ちゃんこ鍋を食べてからの〆（しめ）はラーメンからの雑炊の眼鏡Pです。

＃片方ではなく、両方楽しめる！

数学を「かいせつ」しています。文書とは違って、数学の途中式や図などはＰＣだと入力しずらいため、手書きのものをiPhoneやＰＣに取り込んで編集しています。見づらかったりしたら、すみません…

現在、1番分かりやすいやり方を模索中です！

では、2023年群馬県入試（後期）の過去問の数学を「かいせつ」していきます。

数学5⃣　関数とグラフの問題

（1）9ｍ

 電車が出発してからx秒後までに地点Ｐから東に進んだ距離をymとすると、20秒後までは、

y=1/4x²・・・ア

の関係があるので、アの式にx=6を代入する。

y=1/4×6²

＝9

電車は出発してから6秒後までに東の方向へ9m進んだことになる。

（2）

①点イ

 図Ⅲのyの値（縦軸）は、地点Pから東に進んだ距離を表す。

なので、和也さんが電車より前を走っていることを表す点は、同じxの値において、和也さんのグラフのyの値が、電車のグラフのyの値より大きい点である。

【眼鏡Ｐ訳】

2のグラフを見たときに

和也さんのグラフが上にあれば、和也さんが電車より前を走っている

和也さんのグラフが下にあれば、和也さんが電車より後ろを走っている

ア→×（和也さんのグラフが下になっている）

イ→〇（和也さんのグラフが上になっている ）

ウ→×（和也さんのグラフが下になっている ）

②25/3 （m）

 電車が地点Pを出発してから10秒後に同じ地点を走っていた地点を地点Rとする。 

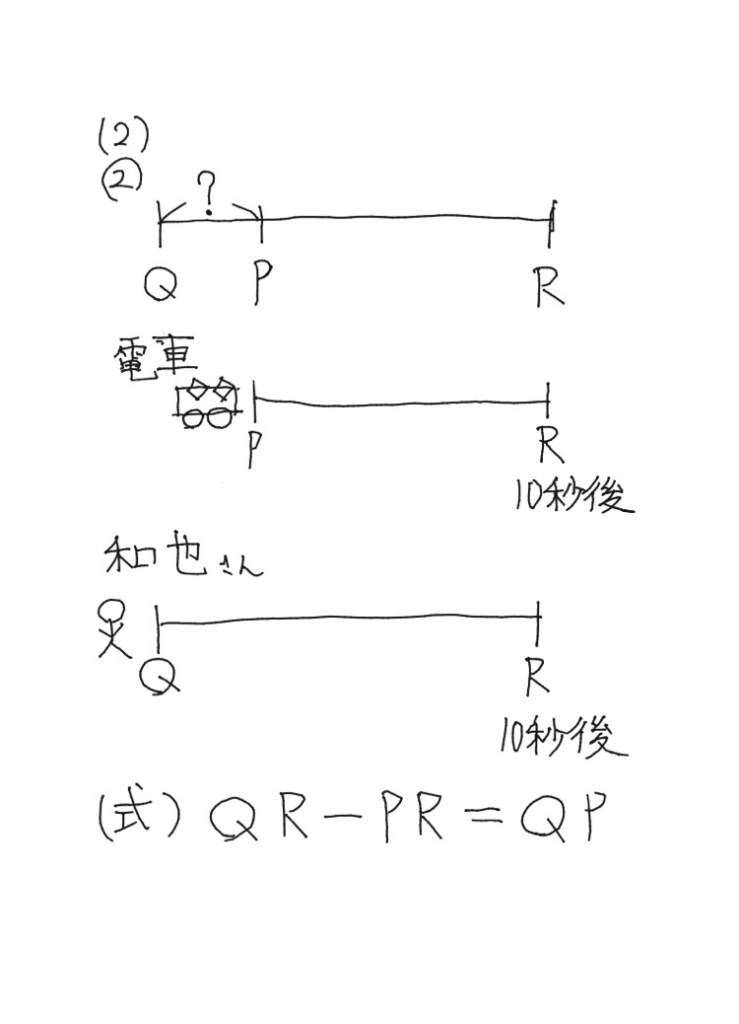
地点P→電車の通過地点

地点Q→和也さんの通過地点

地点R→10秒後に電車と和也さんが一緒になる地点

QP（地点Qから地点Pまでの距離）は、QR-PRで求められる。

距離QRは

和也さんは、毎秒10/3mの速さで地点Qから10秒後に地点Ｒを走っていたから、

QR=10/3×10

　 ＝100/3

QR=100/3（ｍ）

距離PRは

電車は、y=1/4x² の速さで地点Pから10秒後に地点Ｒを走っていたから、

y=1/4x²にx＝10を代入して、

y=1/4×10²

 ＝25

PR=25（m）

よって、地点Qから地点Pまでの距離は、

QP=QR-PR

　  =100/3-25

     ＝25/3

QP=25/3 （m）である。

③和也さんは、地点Qを通過してから地点Ｐを走っている時間は

距離÷速さ＝時間のため

ＱＰの距離÷和也さんの速さ＝地点Qを通過してから地点Ｐを走っている時間となる。

よって、

25/3÷10/3

＝5/2（秒後）に地点Pを走っている。

このとき、電車は地点Pからの距離は先ほどだした5/2秒を代入すれば求められるため

1/4×（5/2）²

=25/16（m）の地点を走っている。

よって和也さんが地点Ｐを走っていたときの、和也さんと電車との距離は25/16（ｍ）である。

以上になります。

※意味や画像などはWikipediaなどのインターネットを参照しています。

2023年　群馬県　公立高校入試　過去問　数学の5⃣でした。次回はこの続きを「かいせつ」していきます。

よろしくお願いいたします！