友達に会うと必ず「その服装で寒くないの？」と聞かれるの眼鏡Pです。
＃ミートテックなめるなよ（笑）

数学の途中式や図などはＰＣだと入力しずらいため、手書きのものをiPhoneやＰＣに取り込んで編集しています。見づらくて、すみません…

現在、1番分かりやすいやり方を模索中です！

では、2023年群馬県入試（後期）の過去問の数学を「かいせつ」していきます。

数学6⃣　平面図形

（1）ア、二等辺・イ、AOD・ウ、中心

ア
CO＝CDより2辺が等しい三角形は「二等辺三角形」

イ
二等辺三角形の底角は等しいため「＜AOD」
ちなみに＜CODだと不正解になると思われる。
※これは採点者にもよるが、
・＜AOD＝1/2＜EODの証明のため、＜CODだと＜AOD＝＜CODとまた元に戻さないといけないから
・①では、＜CDOではなくて、＜EDFとなっているため

ウ
円周角と中心角の関係のため

（2）
いつもは解説をもとにしていますが、今回の問題は少しでも分かりやすいよう、眼鏡P独自の「かいせつ」にしています。

①30°

1、まずは＜EDF＝＜EOB

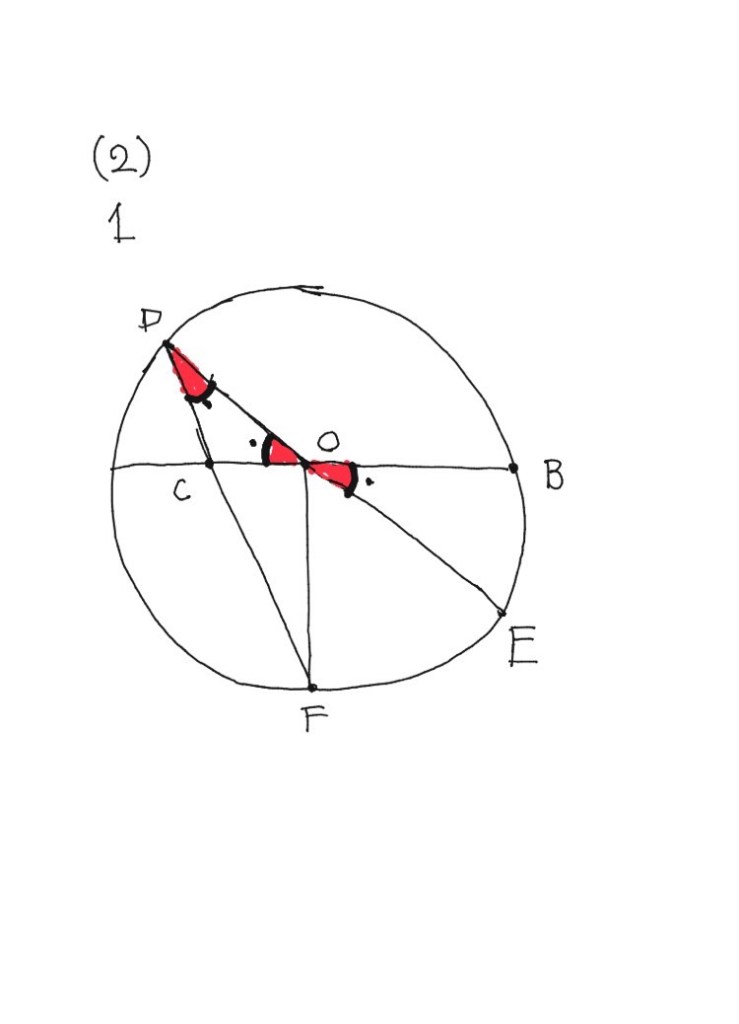
2、次に＜EDF×2＝＜FOE

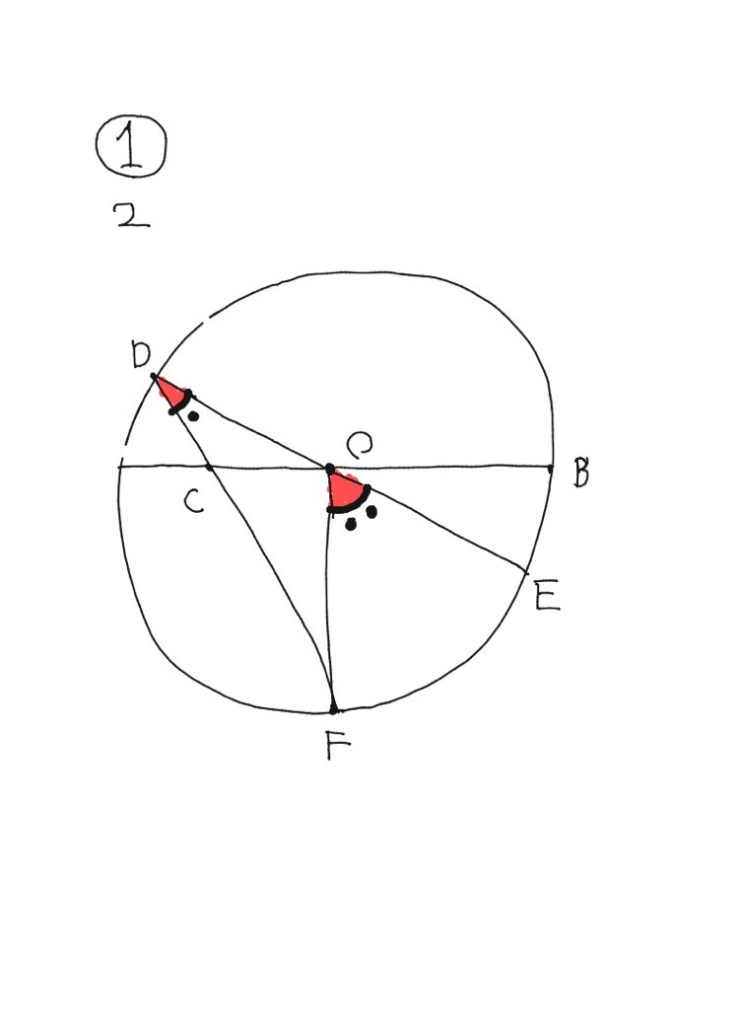
3、よって＜BOF＝＜EDF×3

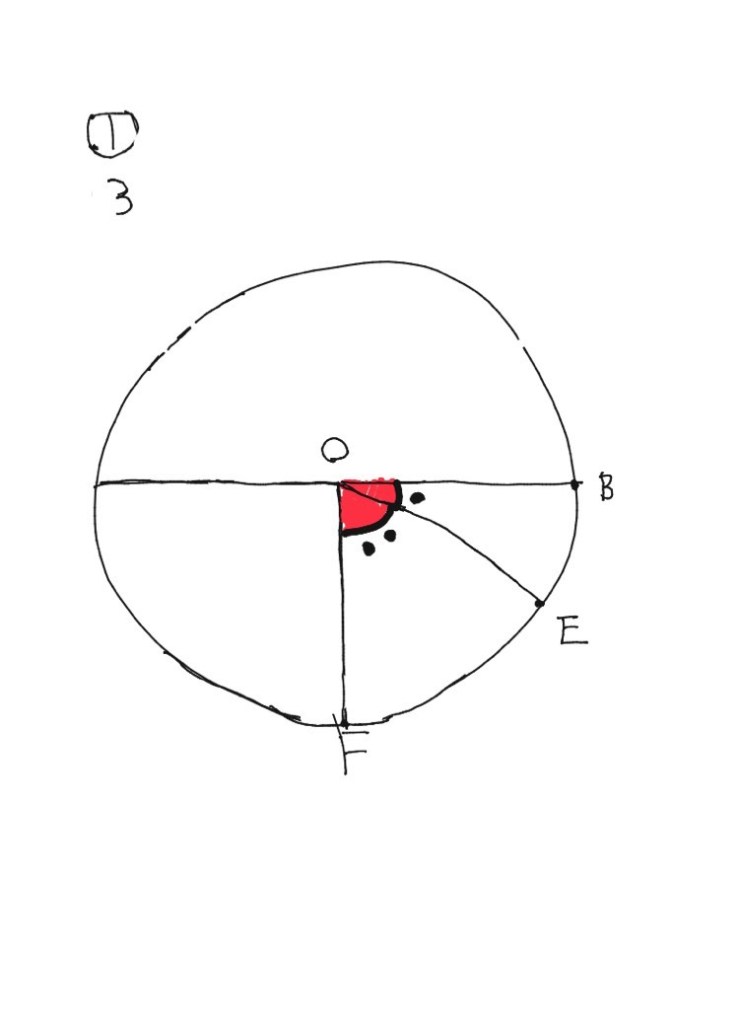
4、計算する
＜BOF＝90°であり、＜ＥＤＦの3個分の大きさのため、
＜EDF＝90÷3
　　 ＝30°

②2√3（ｃｍ）

1、△COFがポイント
そのためにも円Cに注目すると、中心角と円周角の関係で＜OCF＝60°である。

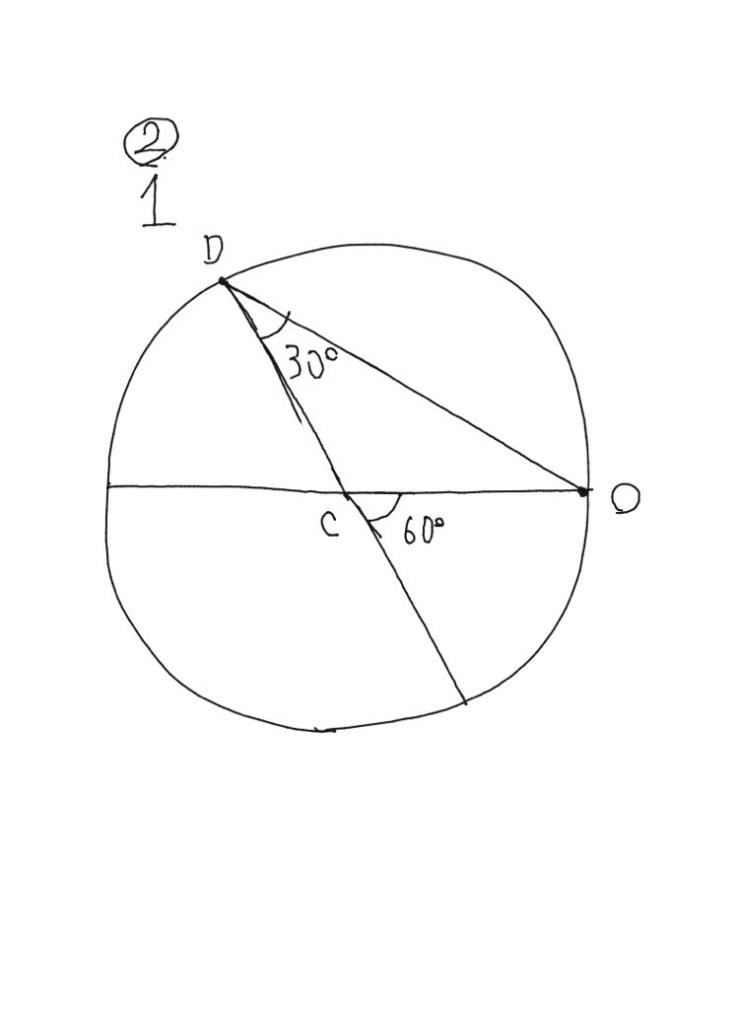
2、△COFが直角三角形！しかも、30°と60°の！

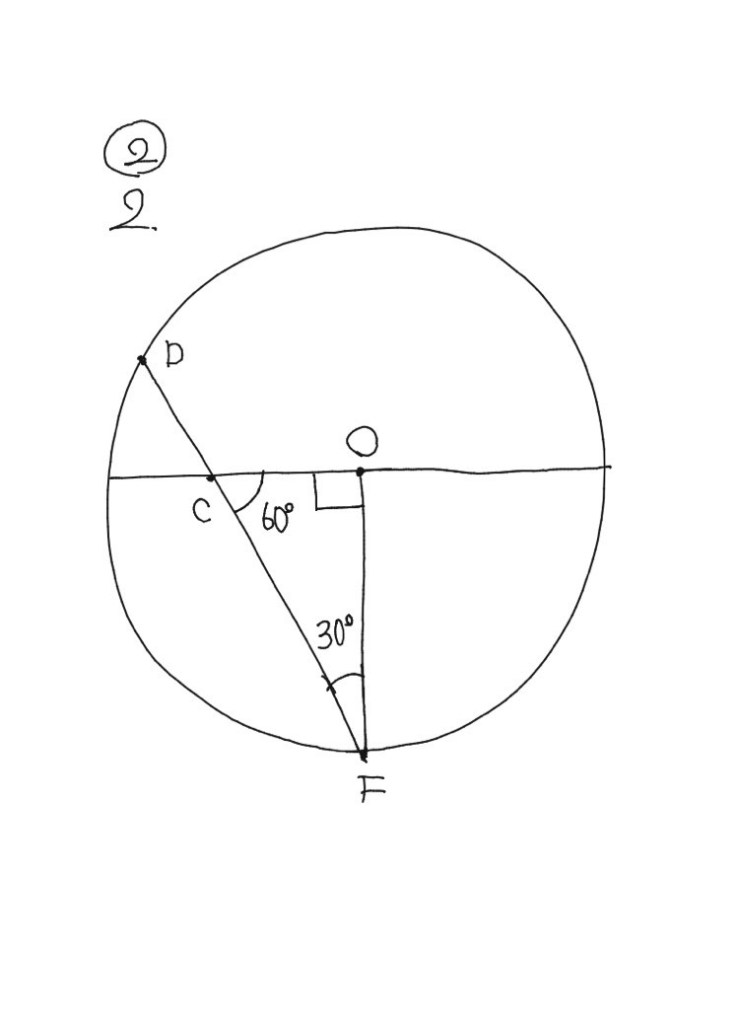
3、30°、60°の直角三角形は1：2：√3

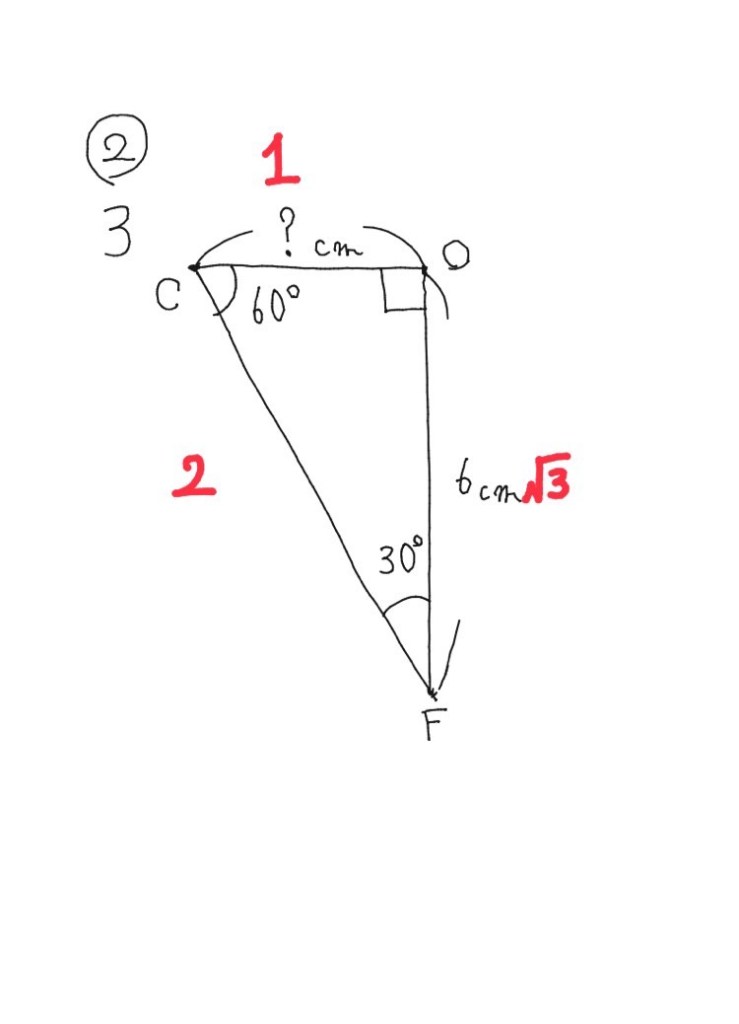
4、OF＝6ｃｍのため、
1：√3＝？：6
よって、2√3ｃｍ

③6√3-2π（ｃｍ²）

1、円Cに注目！
まずは分かりやすく、点OAを伸ばして、半分にしてみる。交点は点Ｆとする。
斜線しているDFAの部分を出すには、
DFOの面積からDAOの面積を引けばよさそう！

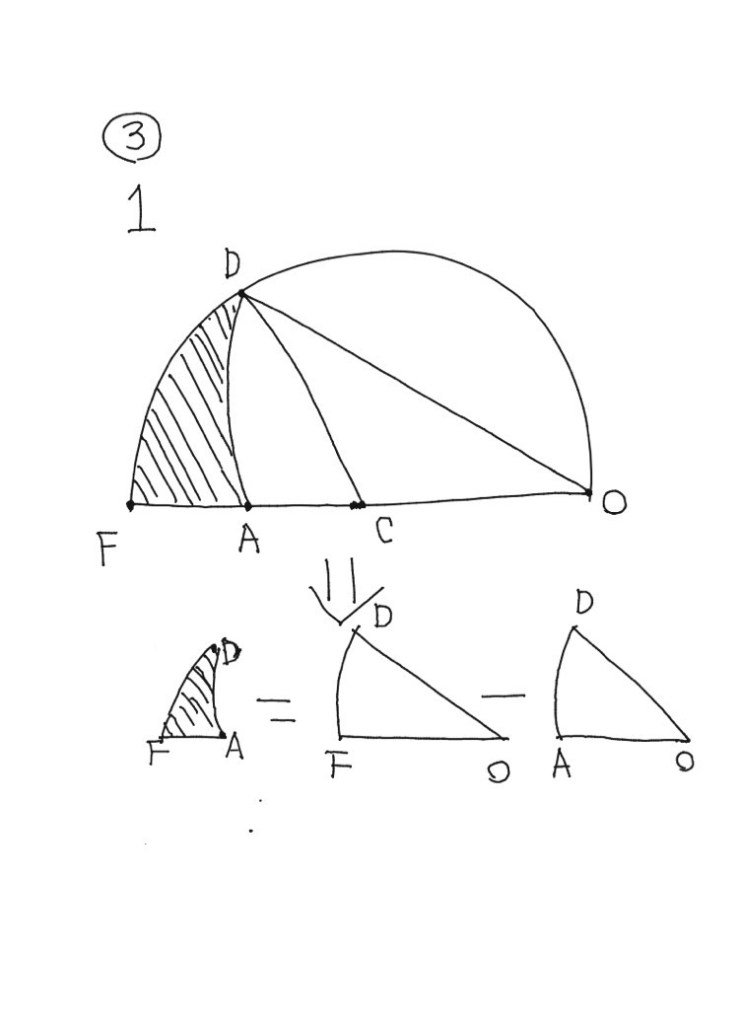
2、DＦOの面積はⅠとⅡと分けて考えると求めやすい。

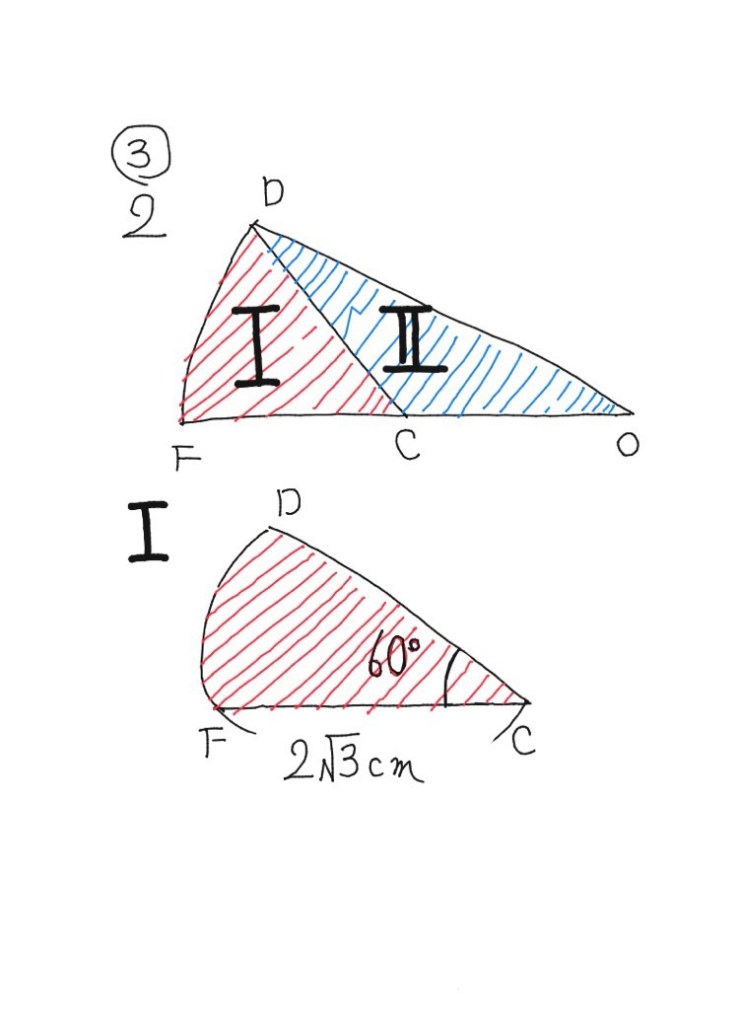
Ⅰ：DFC
2√3×2√3×60/360×π
=2π（ｃｍ²）

3、二等辺三角形は真ん中に線を下す。その点をＧとすると、直角になる。30°と60°の直角三角形のため、1：2：√3の計算ができる。

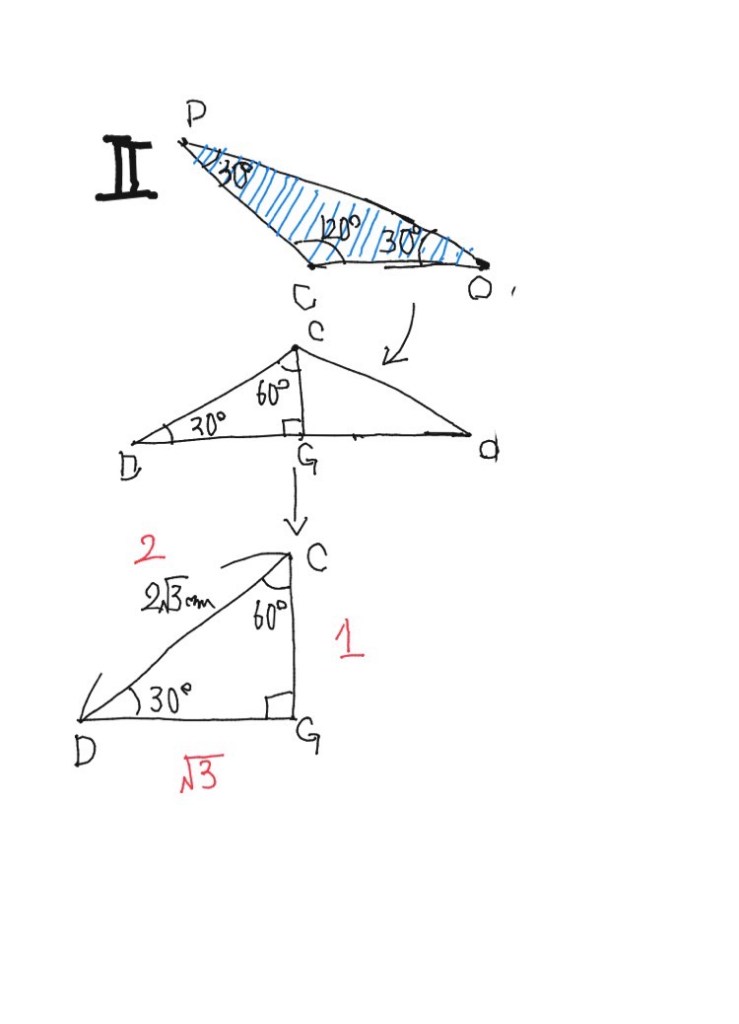
Ⅱ：ＤＣＧ
ＣＤ＝2√3cmのため、ＣＧ＝√3cm、ＤＧ＝3cmとなる。よって面積は
√3×3×1/2＝3√3/2が2つあるため、
3√3/2×2＝3√3

よって、ＯＦＤはⅠ+Ⅱのため
ＯＦＤ＝2π+3√3（ｃｍ²）となる

4、DＡOの面積はⅢとする。

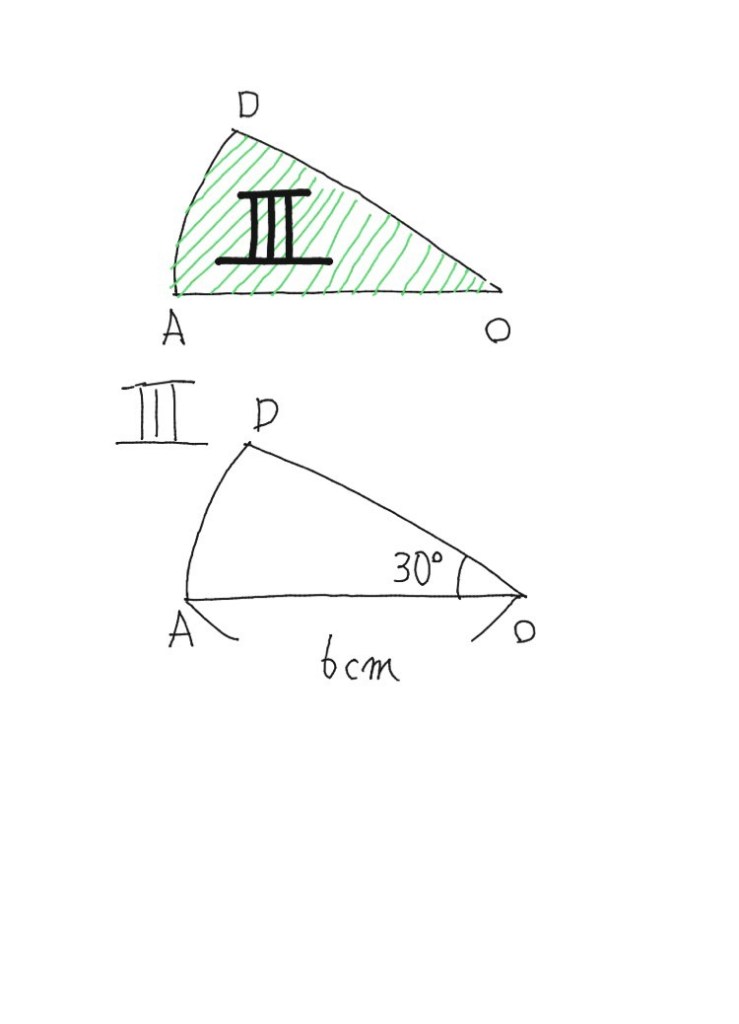
Ⅲ：DＡＯ
6×6×30/360×π＝3π（ｃｍ²）

5、計算すると
DFA=DFOーDAO
　　=（3√3+2π）ー3π
　 ＝3√ーπ（ｃｍ²）

答えはこれが2つ分の大きさのため、
（3√3ーπ）×2
＝6√3ー2π（ｃｍ²）

以上になります。

※意味や画像などはWikipediaなどのインターネットを参照しています。

2023年　群馬県　公立高校入試　過去問　数学の6⃣でした。次回は英語を「かいせつ」していきます。

よろしくお願いいたします！