こんばんは！

「すずめの戸締り」で大号泣した眼鏡Pです。
＃マジすごすぎるわ。新海さん（笑）

では、2022年群馬県入試（後期）の過去問のを数学を「かいせつ」していきます。

ペンタブに慣れてなさ過ぎて、字は読みづらくてすみません！
だんだん図形を入れたり、文字を入力したりと工夫できるように成ってきました！
＃おそ（笑）

頑張ります！

数学4⃣（証明、作図の問題）

4 （形の証明、作図）
△OCEと△ODEにおいて
手順Ⅰより、OC＝OD・・・①

手順Ⅱより、CE=DE・・・ ②

OEは共通・・・ ③

①、②、③より、3組の辺がそれぞれ等しいから

△OCE≡△ODE

かいせつ
①同じ円の半径の長さは等しい
②同じ円の半径の長さは等しい
③共通（同じってこと）

（2）
※ポイント
作図は基本3パターンでできている！
①垂線（特徴：点と線が垂直で交わる）
②垂直二等分線（特徴：引いた線に対して、点と点の距離が等しい）
③角の二等分線（特徴：引いた線に対して、線と線の距離が等しい）

今回の問題は、
四角形ABCDの辺BCが辺AD上に重なるように折りたい！
⇓
辺BCと辺ADを重ねたい！
⇓
重なるってことは、直線PQに対して、辺BCと辺ADの距離が同じだったら、折り曲げたら重なる！
⇓
引いた線に対して、線と線の距離が等しくしたいから・・・
使うのは「③の角の二等分線」だ！
⇓
折り目となる直線PQは、辺BCと辺ADがつくる角の二等分線！

（作図手順）次の①～③の手順で作図する。

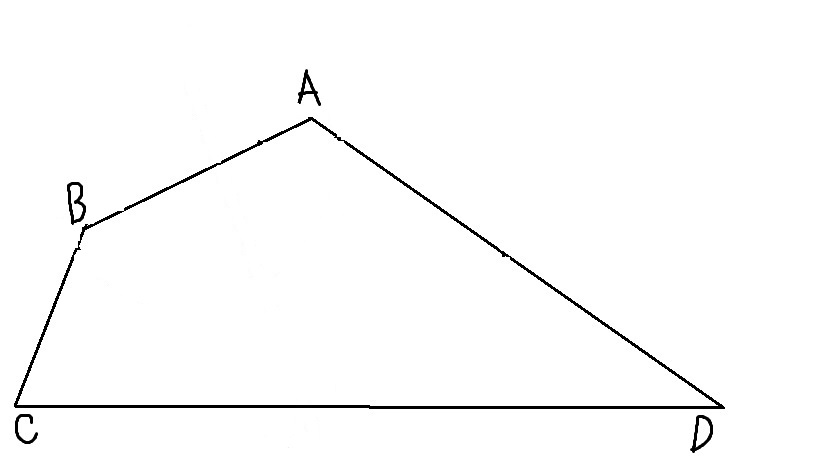
①辺BC，ADをそれぞれ延長して、交点Oとする。

②点Oを中心とした円を描き、辺BC,AD上に交点をつくる。

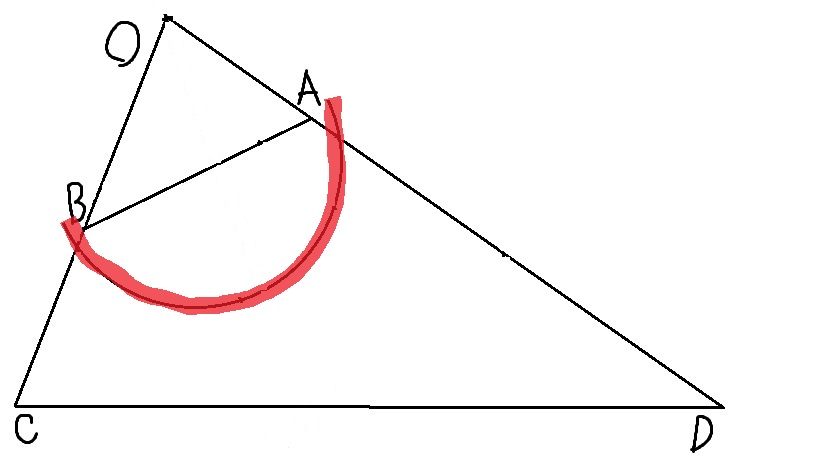
③ ②でつくったそれぞれの交点を中心として、交わるように半径の等しい円を描く。

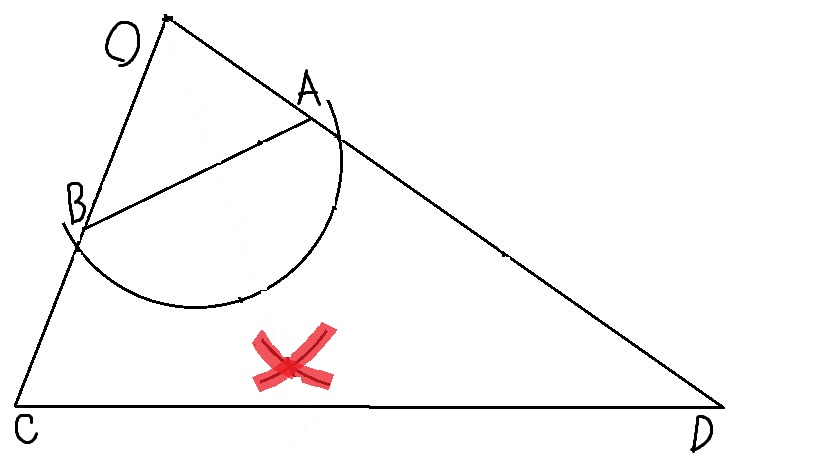
④その交点と点Oを通る直線（＜BOAの二等分線）を引き、正方形の折り紙の辺との交点をP、Qとする。

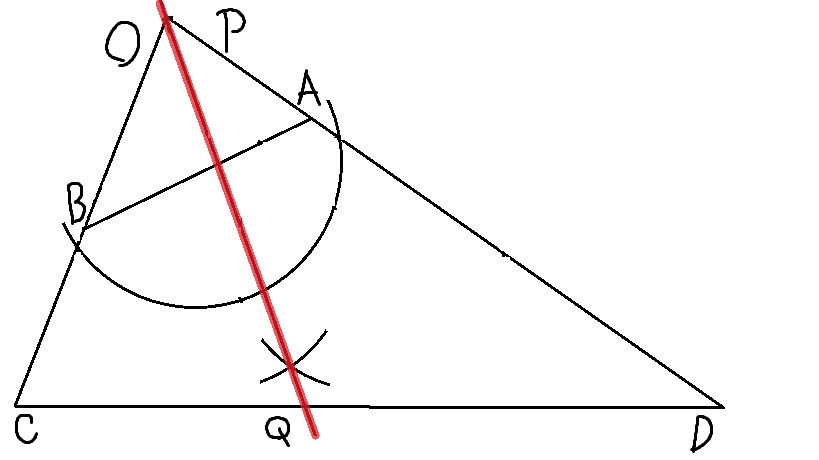
【解答】（解答用紙には点Oの表記は不要）

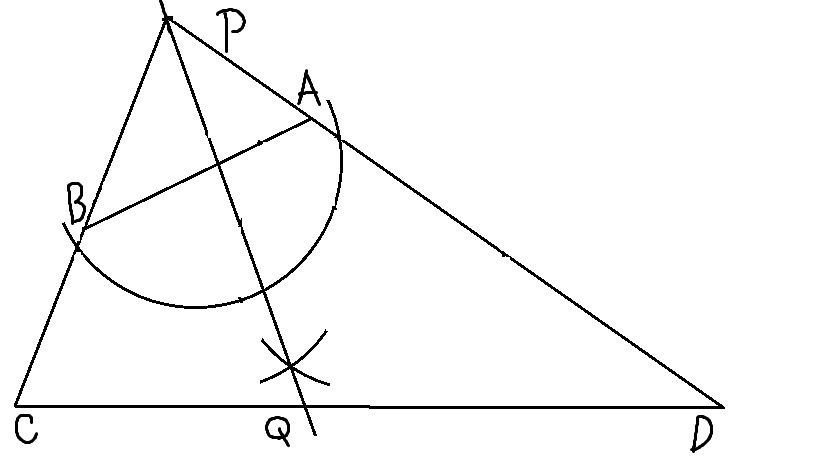
以上になります。
※意味や画像などはWikipediaなど、さまざまなサイト様を参考にさせていただいています。
どれもこれも分かりやすいです！ありがとうございます！

本日もご覧くださり、ありがとうございました！
2022年　群馬県　公立高校入試　過去問　数学でした。明日からはこの続きをやっていきます！

よろしくお願いいたします！