こんばんは！

数学の動点の問題、マジでヤバいなと思ってるけどそろそろ終わらせないと思っている眼鏡Pです。
＃動点、増やすなよ・・・・泣
＃あるあるだけどね（笑）

では、2022年群馬県入試（後期）の過去問のを数学を「かいせつ」していきます。

ペンタブに慣れてないのですが、だんだん図形を入れたり、文字を入力したりと工夫できるように成ってきました！
#スピードはまだまだです。
＃頑張ります！

数学6⃣（動点の問題）

（3）
ｘ＝6のときｙ＝24/5
ｘ＝28/3のときｙ＝112/15

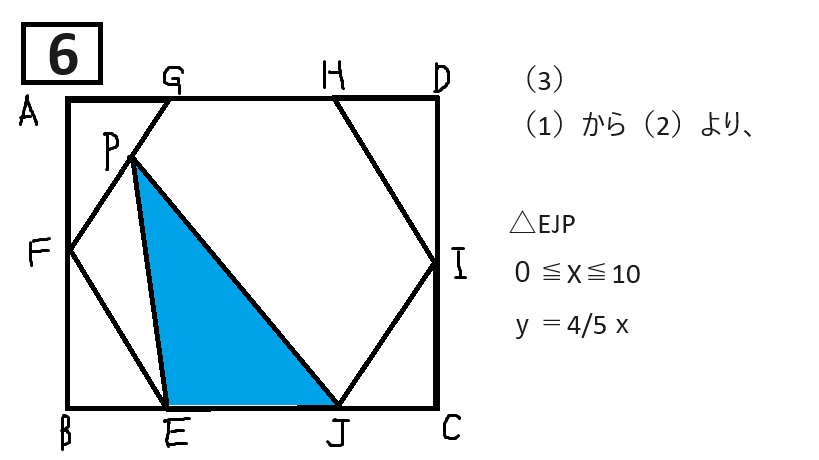
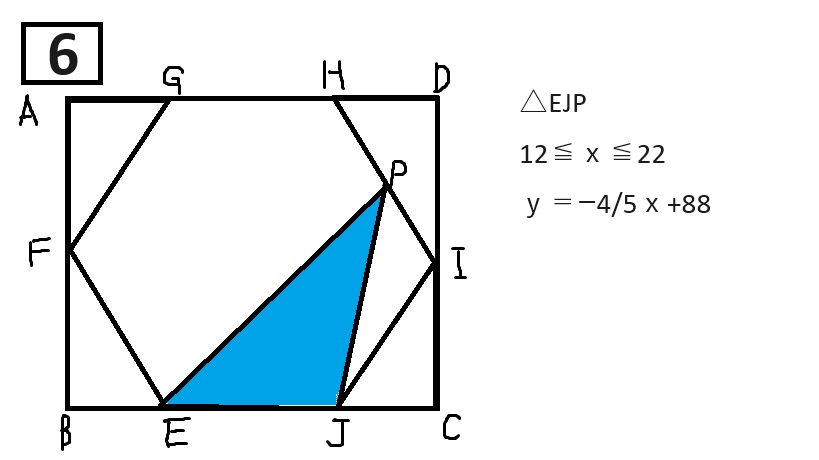
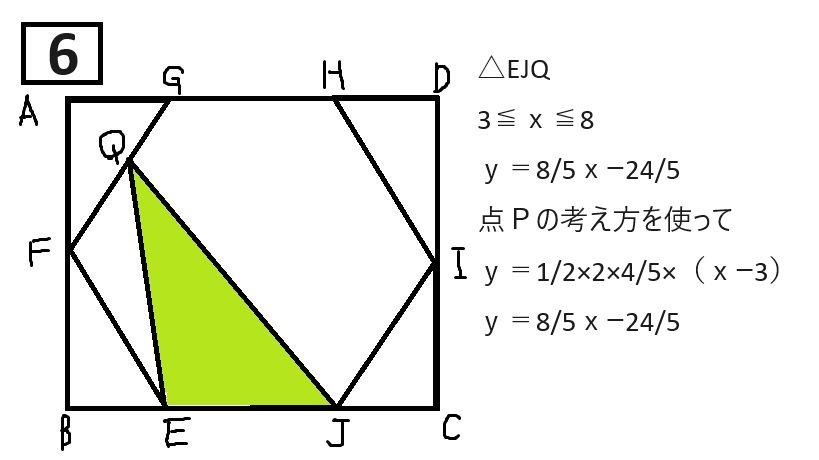
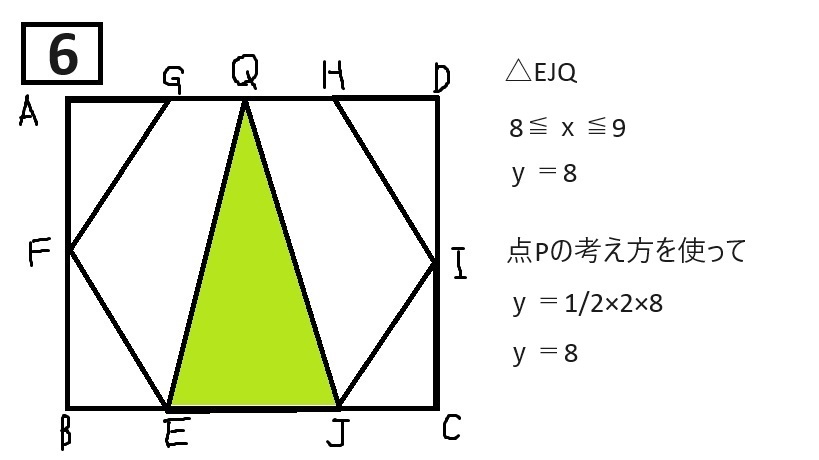
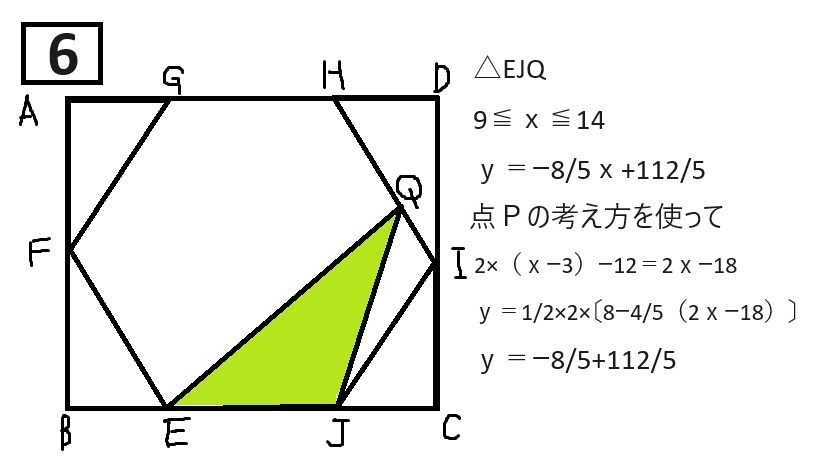
【解説に載っているグラフ】（写真なので、詳しくはぜひ過去問を見てください！）

まとめると
△EJPの面積
①0≦ｘ≦10（ｙ＝4/5ｘ）
②10≦ｘ≦12（ｙ＝8）
③12≦ｘ≦22（ｙ＝-4/5ｘ+88/5）

△EJQの面積
①3≦ｘ≦8（ｙ＝8/5ｘ-24/5）
②8≦ｘ≦9（ｙ＝8）
③9≦ｘ≦13（ｙ＝-8/5ｘ+112/5）

ｘの範囲が被っているのは？
3パターン
・△EJP の①と△EJQの①
・△EJP の①と△EJQの②
・△EJP の③と△EJQの①

さらにｙの範囲で被っているのは？
・△EJP の①と△EJQの①→〇
・△EJP の①と△EJQの②→×
（△EJPがｙ＝8になるのは②から）
・△EJP の③と△EJQの①→〇

よって、2パターンに絞り込める！
・△EJP の①と△EJQの①
・△EJP の③と△EJQの①

この2パターンをそれぞれ連立方程式で解くと
・△EJP の①と△EJQの①
ｙ＝4/5ｘ
ｙ＝8/5ｘ-24/5
ｘ＝6のときｙ＝24/5

・△EJP の③と△EJQの①
ｙ＝4/5ｘ
ｙ＝-8/5ｘ+112/5
ｘ＝28/3のときｙ＝112/15

以上になります。
※意味や画像などはWikipediaなど、さまざまなサイト様を参考にさせていただいています。
どれもこれも分かりやすいです！ありがとうございます！

本日もご覧くださり、ありがとうございました！
2022年　群馬県　公立高校入試　過去問　数学でした。
ここらへんで群馬県は終わりにして、今度から他の都道府県にチャレンジする予定です。
＃ようやく（笑）

※お知らせ

すみません！
明日から約3週間くらいWi-Fiが使えなくなります。広島を離れての仕事になります。徳島からフェリーで東京に行ったり、群馬にトンボ帰りしたり、また広島に帰って、すぐに北海道に行ったりとバタバタします。
＃日本中を飛びまわる男！

ご迷惑をおかけして申し訳ありませんが、その間は解説以外で何か発信する予定ですので、お楽しみください。

よろしくお願いいたします！