塾の名前を「そうだ　塾行こう。」にしようか真剣に考えた眼鏡Pです。
＃広告のパクリ（笑）
＃さぁ、京都行こう。

では、2023年広島県公立高校入試の過去問の数学を「かいせつ」していきます。

数学2⃣（小問集合）

（1）0≦ｙ≦20

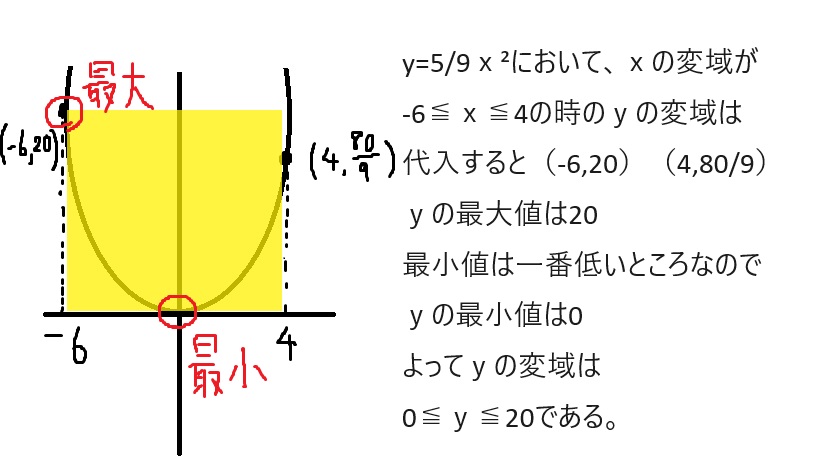
（2）150
※写真はテキストから抜粋したものになります。

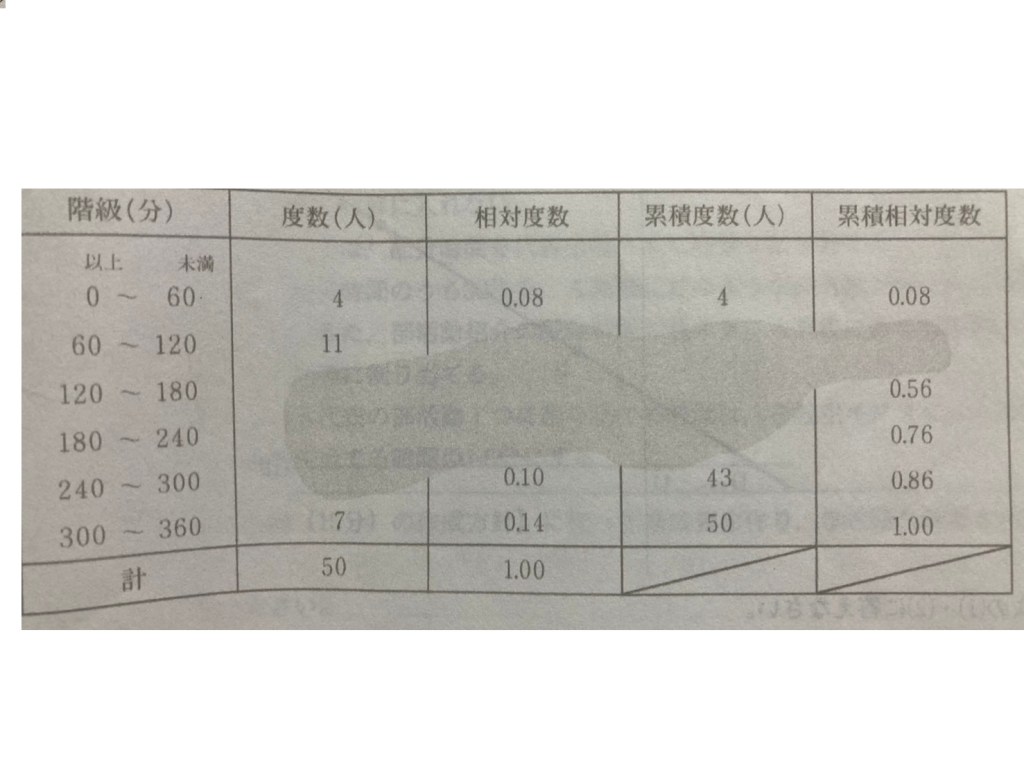
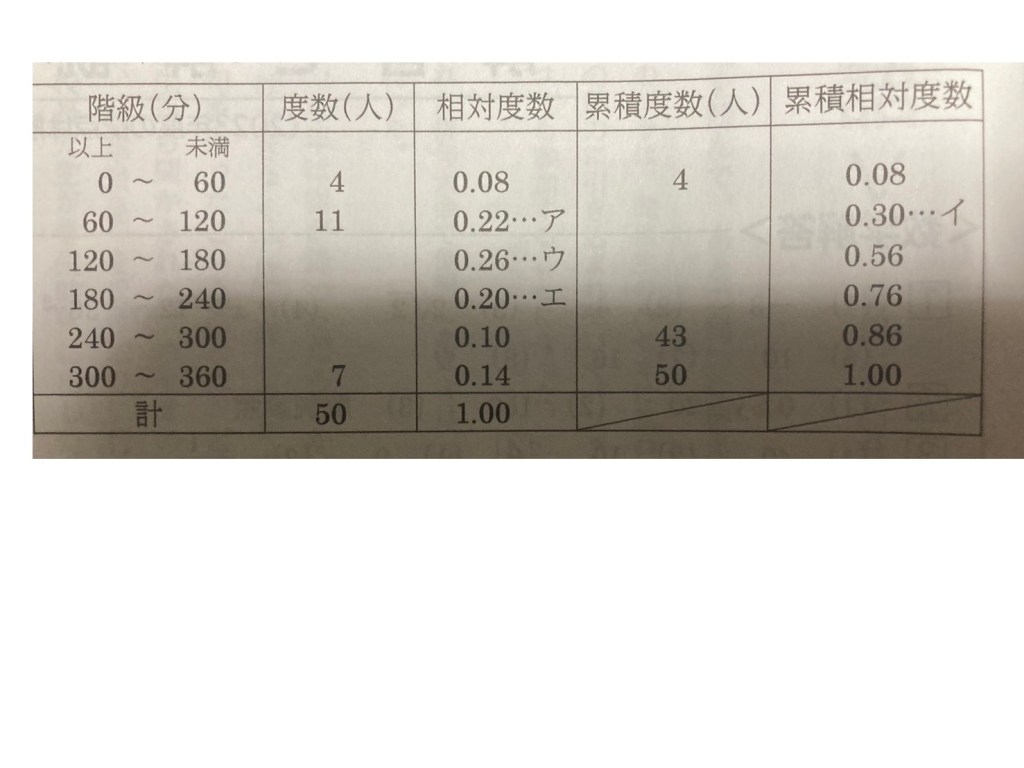
解きやすい順番は
イ：（11+4）÷50＝0.30
ア：0.30ー0.08＝0.22
ウ：0.56ー0.30＝0.26
エ：0.76－0.56＝0.20
よって、度数が多いのは相対度数が一番大きいため0.26が一番大きい。
この時の階級は120分以上～180分未満のため、
（120+180）÷2＝150

ちなみに度数（人）は上から、4人、11人、13人、10人、5人、7人である。
累積度数は上から、4人、15人、28人、38人、43人、50人である。

（3）

（例）
＋の位の数がa、一の位の数がbの2桁の自然数は10a＋bと表すことが出来る。
よって、＋の位の数と一の位の数を入れかえた自然数は10b＋aと表す。

もとの自然数を4倍した数と、入れかえた自然数を5倍した数の和は、

4（10a＋6）+5（10b＋α）
＝45a+54b
＝9（5a＋6b）

5a＋6bは整数だから、9（5a＋6b）は9の倍数である。

したがって、もとの自然数を4倍した数と、入れかえた自然数を5倍した数の和は、9の倍数になる。

以上になります。
※意味や画像などはWikipediaなど、さまざまなサイト様を参照しています。

本日もご覧くださり、ありがとうございました！

2023年　広島県　公立高校入試　過去問　数学でした。次回からはこの続きを「かいせつ」していきます。

よろしくお願いいたします！