暑すぎて頭が回らない眼鏡Pです。
＃最近の暑さ、ヤバすぎでしょう笑

では、2022年広島県公立高校入試の過去問の数学を「かいせつ」していきます。

数学1⃣（小問集合）

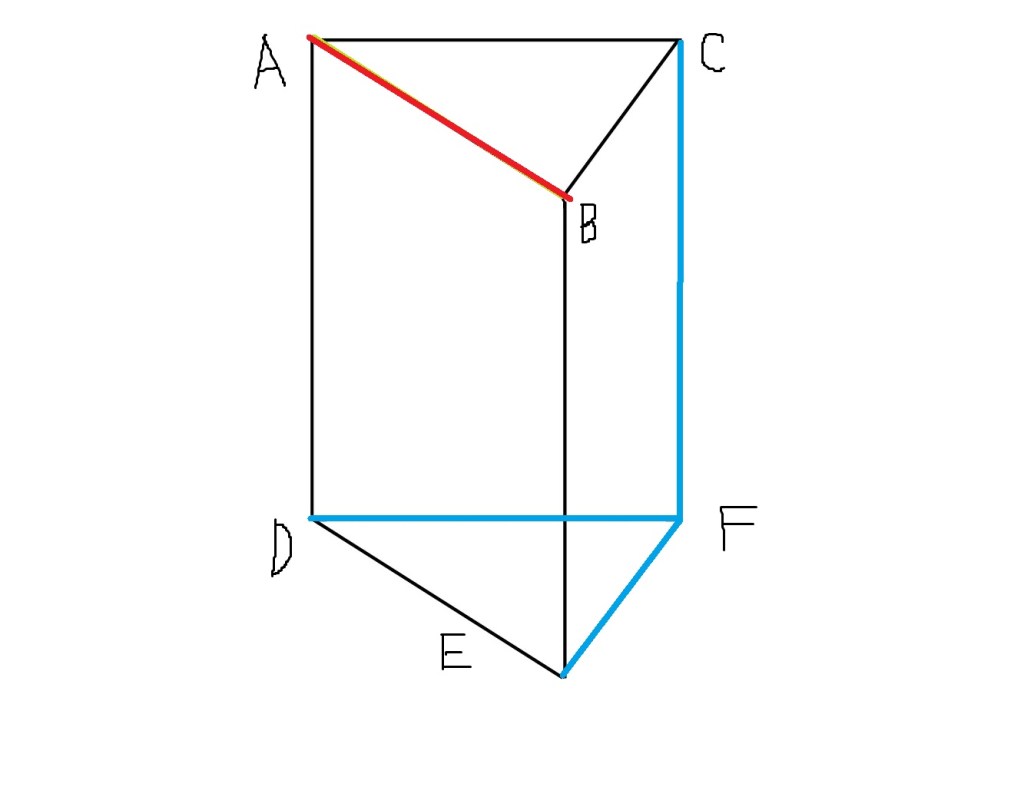
（5）辺CF，辺DF，辺EF
空間内で、平行でなく、交わらない2つの直線はねじれの位置にあるという。辺ABと平行な辺は、辺DEの1本。辺ABと交わる辺は、辺AC，辺AD，辺BC，辺BEの4本。辺ABとねじれの位置にある辺は、辺CF，辺DF，辺EFの3本。

（6）ー6
ｘとｙとの関係が定数aを用いてｙ＝a/xと表されるとき、yとｘに反比例し、そのグラフは双曲線を表す。ｘ＝-3のときｙ＝2だから、これを代入して、a=-6

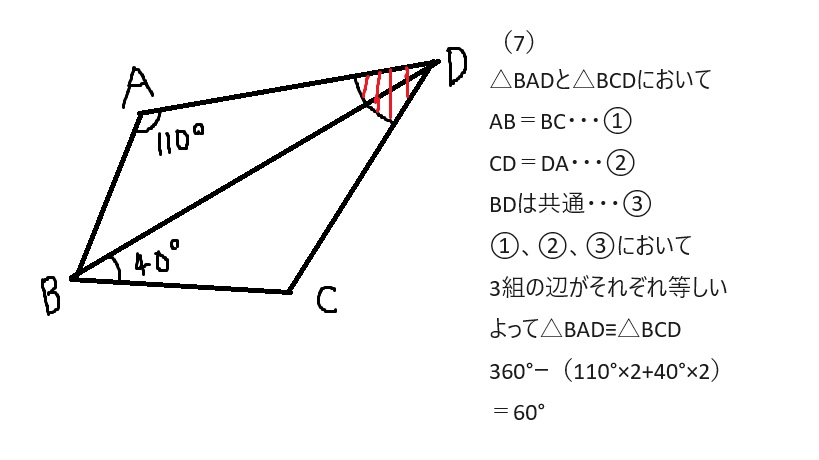
（7）60°

（8）0.35
相対度数＝各階級の度数÷度数の合計
階級は40分以上50分未満のため、度数は14
度数の合計は40
よって14÷40=0.35

以上になります。
※意味や画像などはWikipediaなど、さまざまなサイト様を参照しています。

本日もご覧くださり、ありがとうございました！

2022年　広島県　公立高校入試　過去問　数学でした。次回からはこの続きを「かいせつ」していきます。

よろしくお願いいたします！