こんばんわ！

きゅうりとトマトの苗を植える柵を設営した眼鏡Pです。
＃とうとうこの時期が来ました！

では、2023年栃木県公立高校入試問題の過去問の数学を「かいせつ」していきます。

数学2⃣（小問集合）
1　-2±√3

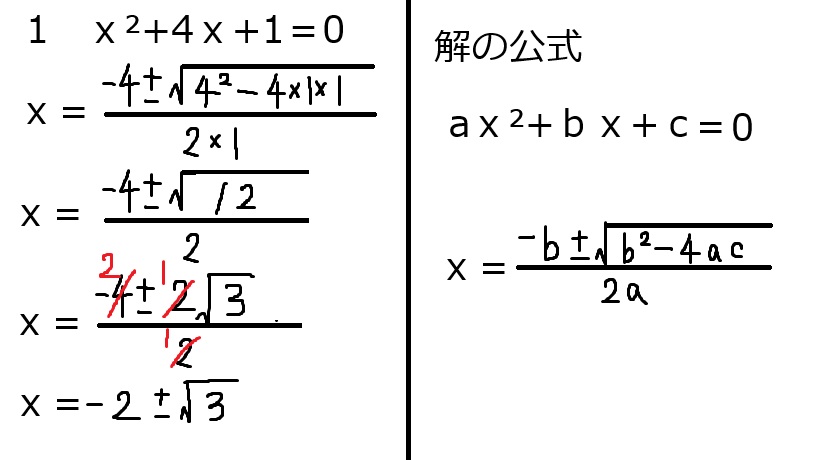
2　12教室

教室の数がｘとしたときに参加者んぼ人数はどうなるかというと、

練習ですが、
たとえば、1教室に10人ずつぴったり入ったら全員で
10×ｘ＝10ｘ
で10ｘ人となります。

では、問題に戻ります。

1つの教室に入る参加者を15人ずつとすると34人が入れないから、参加者の人数は
15×ｘ+34＝15x＋34人となる。

また、1つの教室に入る参加者を20人ずつとすると、
14人の教室が1つ
使用しない教室が1つ

できるから、残りは（ｘ-2）教室となる。
よって20人ずつの教室の数は（ｘー2）教室のため参加者の人数は
20×（ｘー2）+14人＝20ｘ-26人となる。

よって、
15x＋34＝20ｘ-26が成り立つため、これを解くと
15ｘ-20ｘ＝-26-34
-5ｘ＝-60
ｘ＝12

3
【問題】
3けたの自然数Mの百の位、十の位、一の位の数をそれぞれa、ｂ、ｃとすると、
aは1以上8以下の整数、ｂは0以上9以下の整数、cは1以上9以下の整数となる。

このとき、
M=【①】x　a+【②】x　ｂ　+cと表せる。
また、N=M+99より
N=【①】x　a+【②】x　ｂ　+c　+100ー1となるから
N＝【①】×（【③】）+【②】×【④】+【⑤】となり、

Nの百の位の数は【③】、十の位の数は【④】、ーの位の数は【⑤】となる。
よって、Mの各位の数の和とNの各位の数の和はそれぞれ　a　+　b　+　cとなり、同じ値になる。

【かいせつと解答】
3けたの自然数Mの百の位、十の位、一の位の数をそれぞれa、ｂ、ｃとすると、
aは1以上8以下の整数、ｂは0以上9以下の整数、cは1以上9以下の整数となる。

このとき、
たとえば、938だったとき分解すると
100×9+10×3+8と表すことが出来る。
もっと詳しくいうと
100×9+10×3+1×8となり、
100の位は9で10位は3で1の位は8ですよという意味になる。

なので問題もそのまま
M=【①　100】x　a+【②　10】x　ｂ　+cと表せる。

また、N=M+99だから、さっきのMの式をそのままいれると、

N=【100】x　a+【10】x　ｂ　+c　+99
これを少し直して、
N=【100】x　a+【10】x　ｂ　+c　+100ー1
となるから
並び替えると
これを少し直して、
N=100　x　a　+　100　+　10x　ｂ　+cー1
N=100　x　a　+　100　×　1+　10x　ｂ　+cー1
N=100　（　a　+　1）+　10　x　ｂ　+　cー1
よって
N＝【①100】×（【③a　+　1】）+【②10】×【④ｂ】+【⑤cー1】となり、

Nの百の位の数は【a　+　1】、十の位の数は【ｂ】、ーの位の数は【ｃー1】となる。
a　+　1　+　ｂ　+　ｃー1＝a　+　b　+　cのため、

Mの各位の数の和とNの各位の数の和はそれぞれ　a　+　b　+　cとなり、同じ値になる。

以上になります。
※意味や画像などはWikipediaなど、さまざまなサイト様を参考にしています。

本日もご覧くださり、ありがとうございました！

2023年　栃木県　公立高校入試問題　過去問　数学でした。次回からはこの続きを「かいせつ」していきます。

よろしくお願いいたします！

【学習塾トモニー】
塾のホームページが完成しました！もし興味がある方はぜひ、見ていただければと思います！完全自作になります！よろしくお願いいたします！