おはようございます！

久々に朝にUP出来た眼鏡Pです。
＃いつも遅くなって申し訳ありません！

では、2023年栃木県公立高校入試問題の過去問の数学を「かいせつ」していきます。

数学4⃣（箱ひげ図）

箱ひげ図の動画です！ぜひ参考にしてみてください！
＃にしても「とある男」さんの授業はどれもめっちゃ分かりやすい（笑）
＃勉強になります！

3
（1）ア、エ
ア→〇
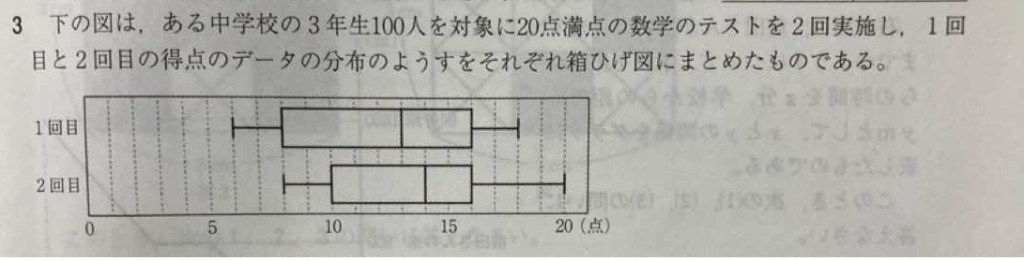
（1回目の中央値は13点、2回目の中央値は14点のため、2回目のほうが中央値は大きくなっているので、正しい。）

イ→×
（最大値は1回目が18点、2回目が20点である。よって2回目のほうが大きいので、誤っている。）

ウ→×
（範囲は、〔最大値〕ー〔最小値）で求められる。
1回目は、最大値が18点、最小値が6点より、18-6=12（点）
2回目は、最大値が20点、最小値が8点より、20-8=12（点）となる。
よって1回目も2回目も同じであるので、誤っている。）

エ→〇
（四分位範囲は、〔第3四分位数〕－〔第1四分位数〕で求められる。
1回目は、第3四分位数が16点、第1四分位数が8点より、16-8=8（点）
2回目は、第3四分位数が16点、第1四分位数が10点より。16-10=6（点）となる。
よって、2回目のほうが大きくなるので、正しい。）

（2）（例）25番目の生徒の得点が7点、26番目の生徒の得点が9点
「1回目のテストで8点を取った生徒がいる」ことが正しくないことを証明する。下の文章の【　　　　　】に当てはまる文を考える。

ちなみに文章は
「箱ひげ図から、1回目の第1四分位数が8点であることがわかるが、8点を取った生徒がいない場合も考えられる。例えば、テストの得点を小さい順に並べたときに
【　　　　】の場合も、第1四分位数が8点となるからである。」
となっている。

生徒数が100人だから、
第1四分位数は、得点が小さい方50人の中央値である。
つまり、第1四分位数は、小さい方から25番目の得点と26番目の得点の平均値である。25番目の得点と26番目の得点が8点でなく、平均値が8点となる場合を考えると、
（例）「25番目の生徒の得点が7点、26番目の生徒の得点が9点」となる。

以上になります。
※意味や画像などはWikipediaなど、さまざまなサイト様を参考にしています。

本日もご覧くださり、ありがとうございました！

2023年　栃木県　公立高校入試問題　過去問　数学でした。次回からはこの続きを「かいせつ」していきます。

よろしくお願いいたします！

【学習塾トモニー】
塾のホームページが完成しました！もし興味がある方はぜひ、見ていただければと思います！完全自作になります！よろしくお願いいたします！