おはようございます！

「長野県は海が無いから川では泳がないんだって」と聞いた眼鏡Pです。
＃それはさすがに偏見でしょう（笑）

では、2023年栃木県公立高校入試問題の過去問の数学を「かいせつ」していきます。

数学5⃣（関数）

2

【問題】
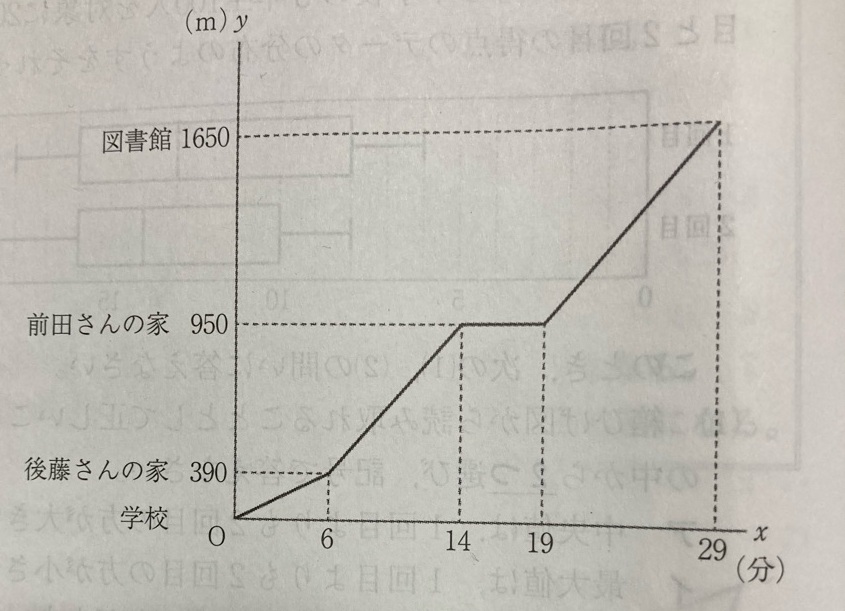
ある日の放課後、前田さんと後藤さんは2人で学校から1650ｍ離れた図書館に行くことにしました。
（ちなみに、上の図は前田さんのグラフになります。）
↓
①前田さんと後藤さんは2人で学校から歩いて、ちょうど6分後に後藤さんの家に着きました。
↓
家に到着すると後藤さんは家で準備をするため、2人はここで一旦、お別れました。
（※後藤さんは（3）で再び登場します。）
↓
②前田さんは1人で毎分70mの速さで8分間歩いて自分の家に着きました。
↓
③前田さんは家に着くと、準備があったので5分休みました。
↓
④その後、前田さんは自分の家から出ると毎分70mの速さで図書館に向かいました。

グラフにまとめるとこんな感じです！

では、問題に戻ります。

（1）　毎分65ｍ
①のグラフに注目してほしい。2人は学校を出てから6分後に学校から390mの距離にある後藤さんの家に着いた。よって、このときの2人の速さは、
390÷6=65より、毎分65mである。

（2）y＝70x-30
②のグラフに注目してほしい。前田さんは後藤さんの家について、後藤さんと別れた。前田さんが自分の家に着くまでの点は（6、390）と（14、950）を結ぶ線分である。

この2点を通る直線は1次関数のため、
ｙ＝aｘ+ｂと表すことができる。
よって、そこにそれぞれの点を代入して連立方程式で解けばいい。

（6、390）を代入すると
390＝6a+ｂ
6a+ｂ＝390・・・①

（14、950）を代入すると
950＝14a+ｂ
14a+ｂ＝950・・・②

6a+ｂ＝390・・・①
14a+ｂ＝950・・・②
を連立方程式で解くと、
a=70、ｂ＝-30となる。

よって式は
y＝70x-30である。

以上になります。
※意味や画像などはWikipediaなど、さまざまなサイト様を参考にしています。

本日もご覧くださり、ありがとうございました！

2023年　栃木県　公立高校入試問題　過去問　数学でした。次回からはこの続きを「かいせつ」していきます。

よろしくお願いいたします！

【学習塾トモニー】
塾のホームページが完成しました！もし興味がある方はぜひ、見ていただければと思います！完全自作になります！よろしくお願いいたします！