こんにちは！

寝起きの娘から「石！」と言われた眼鏡Pです。
＃「大きくて動かないもの＝だいたい石」ということらしいです（笑）

では、2023年栃木県公立高校入試問題の過去問の数学を「かいせつ」していきます。

数学6⃣（特殊問題）

【問題】

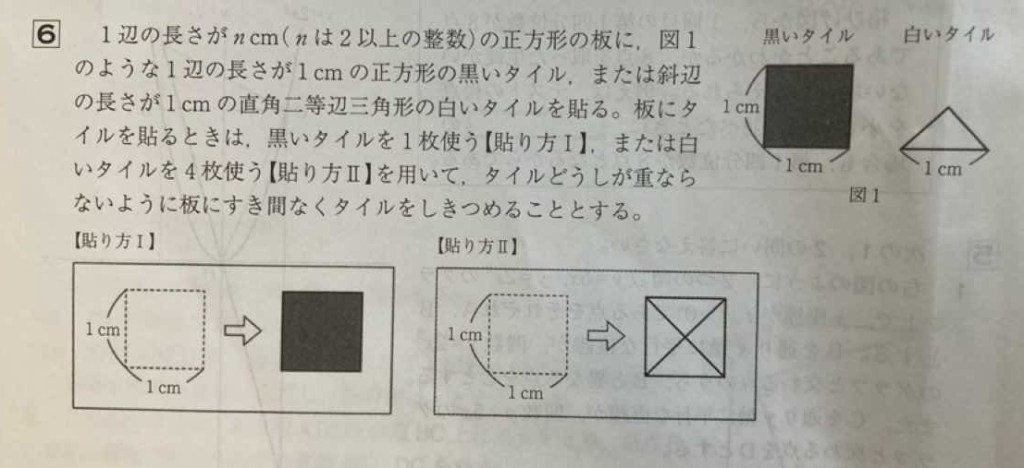
1　64枚
n=4のとき、板は1辺が4cmの正方形となります。
となると、1辺が1cmの正方形は
4✕4=16
16（個）必要となります。

白いタイルは、三角形のため1辺が1cmの正方形を1個作るには4枚必要となります。

よって、白いタイルだけを使うとき、使った白いタイルは
4枚✕16個=64（枚）
よって、ｎ＝4のとき、白いタイルのみで埋めるには64枚必要となります。

2
黒いタイル：17枚
白いタイル：32枚

黒いタイルをｘ枚、白いタイルをｙ枚使ったとする。

問題によると、合計で49枚使ったとのことなので、
ｘ＋ｙ=49・・・・・①

また、n=5のとき、板は1辺が5cmの正方形となります。
となると、1辺が1cmの正方形は
5✕5=25
25（個）必要となります。

1辺が1cmの正方形を作るには
黒いタイルは1枚必要で
白いタイルは4枚必要となるので、
ｘ＋ｙ÷4=25
ｘ+ｙ/4＝25・・・・②

【なんで÷4なの？？】

たとえば、1辺が1cmの正方形を4個作るとき、

●黒い色のタイルの場合
黒いタイルはそのままなので、4枚必要。
4個作るには4枚必要ですし、4枚あれば4個作れます。
ここまでは分かりやすいです。

ただし、白色のタイルは注意が必要です。
●白い色のタイルの場合

たとえば、1辺が1cmの正方形を4個作るとき、
白色のタイルは
4枚×4個＝16枚必要となります。

逆に16枚で1辺が1cmの正方形が何個作れるかでいうと、
1個作るのに4枚必要とするので、
16枚÷4＝4個作れることが分かります。

よって白色のタイルの場合は
1辺が1cmの正方形4個作るには×4して、白いタイルは16枚必要ですし、
逆に白いタイルが16枚あった場合は÷4して、1辺が1cmの正方形4個できる
となります。

だから、÷4をします！


では続きをどうぞ！


①と②を連立方程式で解くと
ｘ＋ｙ=49・・・・・①
ｘ+ｙ/4＝25・・・・②

ｘ＝17、ｙ＝32となる。

よって
黒いタイルは17枚
白いタイルは32枚となります！

以上になります。
※意味や画像などはWikipediaなど、さまざまなサイト様を参考にしています。

本日もご覧くださり、ありがとうございました！

2023年　栃木県　公立高校入試問題　過去問　数学でした。次回からはこの続きを「かいせつ」していきます。

よろしくお願いいたします！

【学習塾トモニー】
塾のホームページが完成しました！もし興味がある方はぜひ、見ていただければと思います！完全自作になります！よろしくお願いいたします！