こんにちは！

娘と予防接種にいくことをデートだと思っている眼鏡Pです。
＃注射、泣かなかったぞ！

では、2022年栃木県公立高校入試問題の過去問の数学を「かいせつ」していきます。

数学1⃣（小問集合）

6　3 π㎝

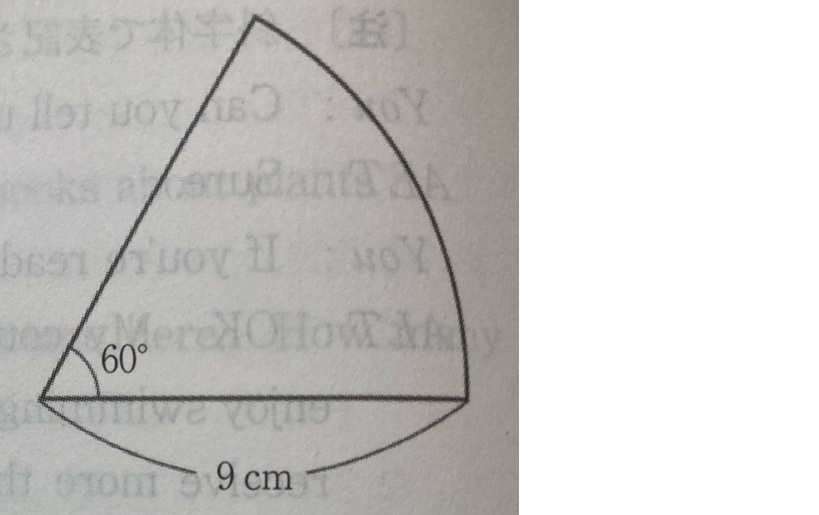
半径が9㎝、中心角が60°のおうぎ形の弧の長さを求めたい。
弧の長さ＝円周×中心角/360
で求められる。

円周＝直径（半径×2）×π
で求められるため、
9×2×π＝18π

よって、
弧の長さ
＝18π×60/360
＝18π×1/6
＝3π

よって、3π（㎝）

7 　61°

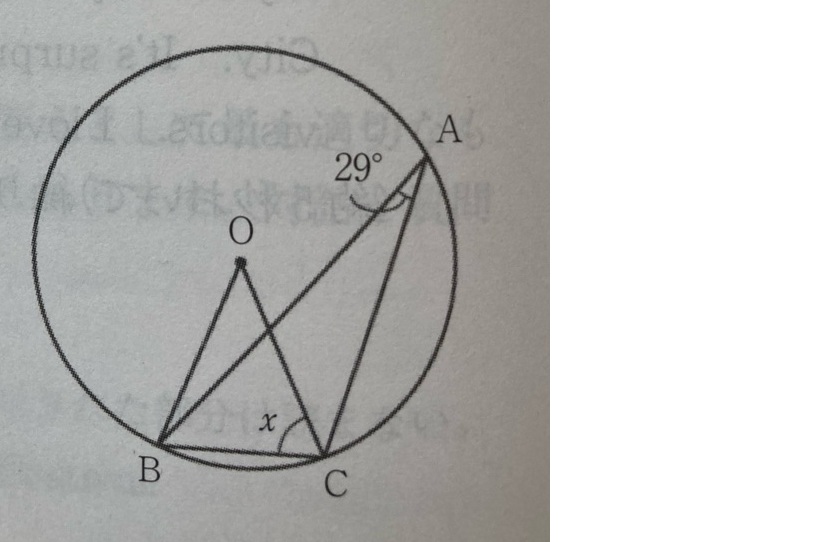
弧BCに対する中心角は弧BCに対する円周角の2倍の大きさになるため、
∠BOC
= ∠BAC ×2
= 29°×2
= 58°
よって、∠BOCは58°である。

△AOBは
半径の長さはみんな同じのため、OB = OCとなる。
よって、 △AOBはOB = OC の二等辺三角形となる。
二等辺三角形の底角は等しいため、
∠OBC = ∠OCBとなる。
三角形の3つの角の和は180°になる。
∠OBC = ∠OCB= x とすると、
∠BOC + ∠OBC + ∠OCB = 180° より、
58° + x + x = 180°
58°+2x = 180°
2x = 180° – 58°
2ｘ= 122°
x = 61°
よって、∠OBC = ∠OCB = 61°である。

8　ウ

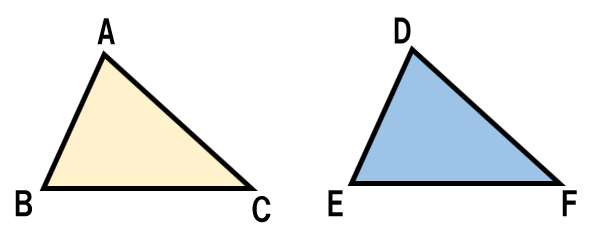
ア→合同
BC＝EC、AB=DE、 AC=DF
3組の辺がそれぞれ等しくなるから、合同である。

イ→合同
BC＝EC、AB=DE、＜B= ＜E
2組の辺とその間の角がそれぞれ等しくなるから、合同である。

ウ→×
BC＝EC、AB=DE、＜C= ＜F
図3の△ABCと△DEFのような三角形が考えられるが、常に合同になるとは限らない。

エ→合同
BC＝EC、＜B= ＜E、 ＜C= ＜F
1組の辺とその両端の角がそれぞれ等しくなるから、合同である。

以上になります。
※意味や画像などはWikipediaなど、さまざまなサイト様を参考にしています。

本日もご覧くださり、ありがとうございました！

2022年　栃木県　公立高校入試問題　過去問　数学でした。次回からはこの続きを「かいせつ」していきます。

よろしくお願いいたします！

【学習塾トモニー】
塾のホームページが完成しました！もし興味がある方はぜひ、見ていただければと思います！完全自作になります！よろしくお願いいたします！