こんにちは！

炎天下の中で草むしりしたら、干からびた眼鏡Pです。
＃太陽、強すぎ（笑）

では、2022年栃木県公立高校入試問題の過去問の数学を「かいせつ」していきます。

数学4⃣（立体図形）

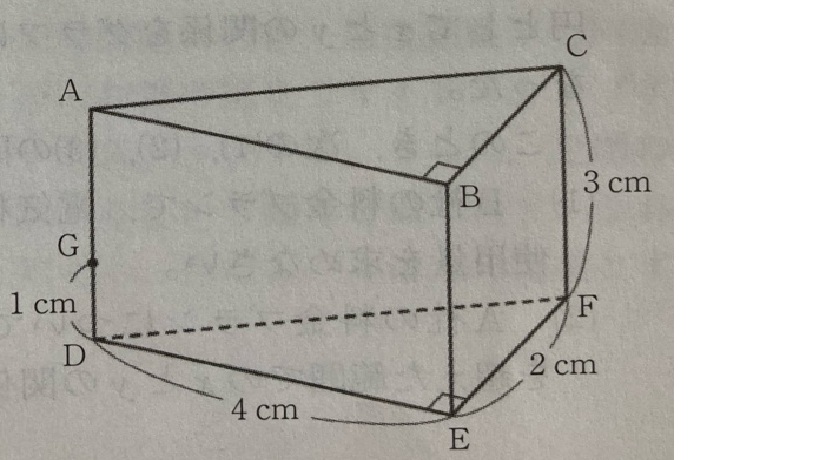
（1）ＢＧ：2√5㎝

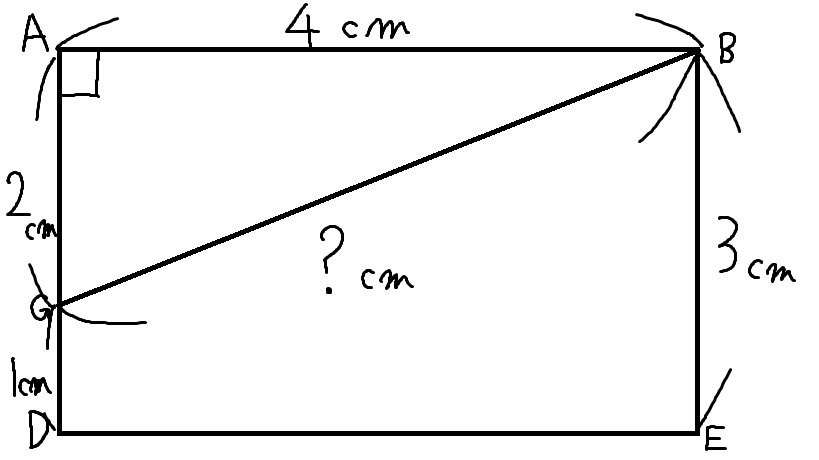
BGの長さを求めるには、△AGBを利用する。
AB＝4㎝

AD＝3㎝
GD＝1㎝
よって
AG＝2㎝

△AGBは＜GAB＝90°のため、直角三角形になる。

BG²=AB²+AG²
BG²=4²+2²
BG²=16+4
BG²=20
BG=2√5

よってBG=2√5㎝になる。

（2）立体の体積：28/3㎤

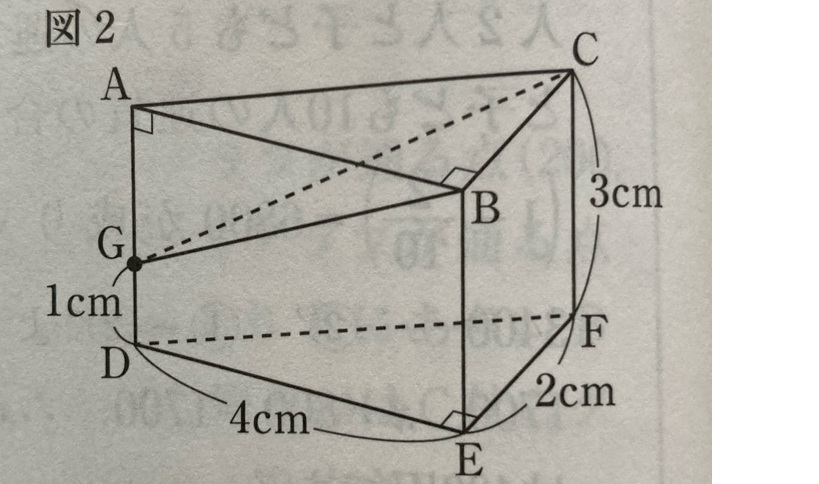
求めたい立体の体積は計算でだすのは難しい。
よって、引いて求める。

立体の体積＝①【三角柱ABC-DEF】ー②【三角錐Ｇ-ABC】

①【三角柱ABC-DEF】
三角柱の体積は
三角柱の体積＝三角形の面積×高さ
三角柱の体積＝底辺×高さ×1/2×高さ

ちなみに、三角形は△ABCのため
三角形の面積は
△ABC＝2×4×1/2
△ABC＝4㎠

そこに高さ（3㎝）をかけるので
三角柱の体積＝三角形の面積×高さ
三角柱の体積＝4×3
三角柱の体積＝12㎤

よって、【三角柱ABC-DEF】の体積は12㎤

②【三角錐Ｇ-ABC】
三角錐の体積は
三角錐の体積＝三角形の面積×高さ×1/3
三角錐の体積＝底辺×高さ×1/2×高さ×1/3

ちなみに、三角形は△ABCのため
三角形の面積は
△ABC＝2×4×1/2
△ABC＝4㎠

そこに高さ（2㎝）をかけるので
三角錐の体積＝三角形の面積×高さ×1/3
三角錐の体積＝4×2×1/3
三角錐の体積＝8/3㎤

よって【三角錐Ｇ-ABC】の体積は、8/3㎤

③立体の体積を求める
・【三角柱ABC-DEF】＝12㎤
・【三角錐Ｇ-ABC】＝8/3㎤

立体の体積＝①【三角柱ABC-DEF】ー②【三角錐Ｇ-ABC】
立体の体積＝12㎤ー8/3㎤
立体の体積＝36/3㎤ー8/3㎤
立体の体積＝28/3㎤

よって求めたい立体の体積は28/3㎤になる。

以上になります。
※意味や画像などはWikipediaなど、さまざまなサイト様を参考にしています。

本日もご覧くださり、ありがとうございました！

2022年　栃木県　公立高校入試問題　過去問　数学でした。次回からはこの続きを「かいせつ」していきます。

よろしくお願いいたします！

【学習塾トモニー】
塾のホームページが完成しました！もし興味がある方はぜひ、見ていただければと思います！完全自作になります！よろしくお願いいたします！