こんばんわ！

上毛かるた（群馬県専用かるた）を買わせていただいた眼鏡Pです。
＃頑張ります（笑）

では、2022年栃木県公立高校入試問題の過去問の数学を「かいせつ」していきます。

数学5⃣（関数）

（1）ｙ＝ーｘ²
ｙ＝ｘ²（青）のｘ軸の対照のグラフはｙ＝ーｘ²（赤）となる。
ｘ軸の線対称はｘ軸を中心に折りたたむと重なるグラフになる。

（2）1/8
△OABと△OCDの面積が等しくなるときのaの値を求める。
まずは△OABの面積を求める。
ｙ＝ｘ²のため、
点A（2，4）
点B（-2，4）
となる。

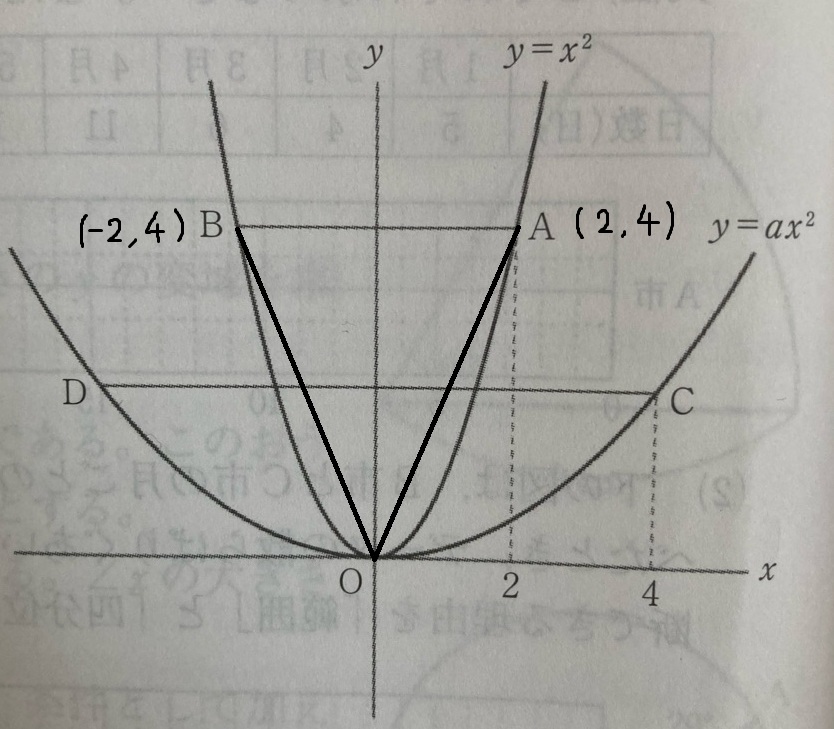
直線AB（底辺）＝4
高さ＝4
三角形の面積＝底辺×高さ×1/2
△OAB＝4×4×1/2
△OAB＝8

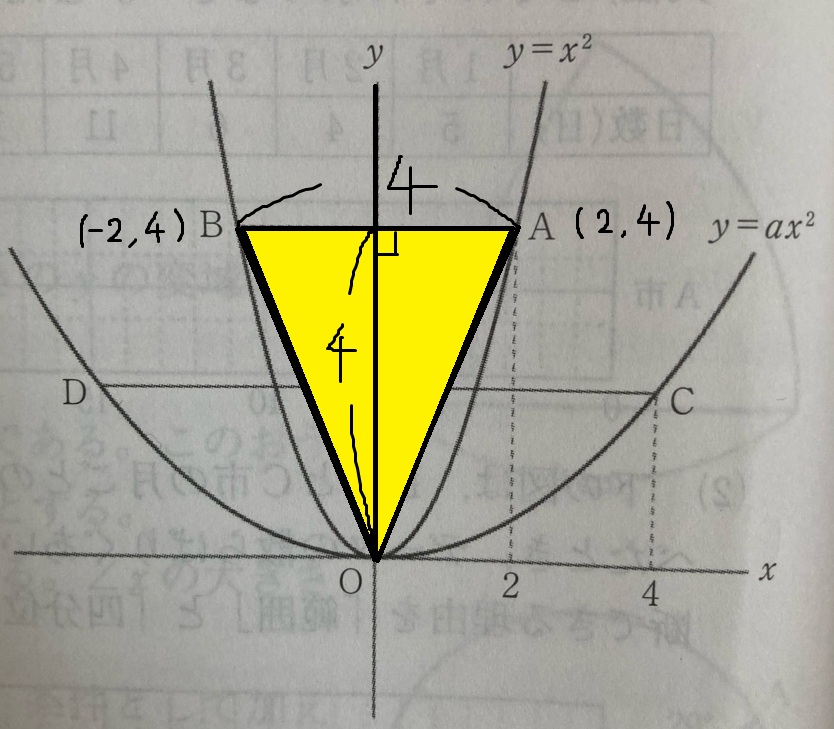
よって、△OABの面積は8

では、次に△OCDの面積はaを使って表すと、
ｙ＝ax²のため、点Ｃのｘ＝4によって代入すると、ｙ＝16aとなる。
同じように点Ｄのｘ＝ー4によって代入すると、ｙ＝16aとなる

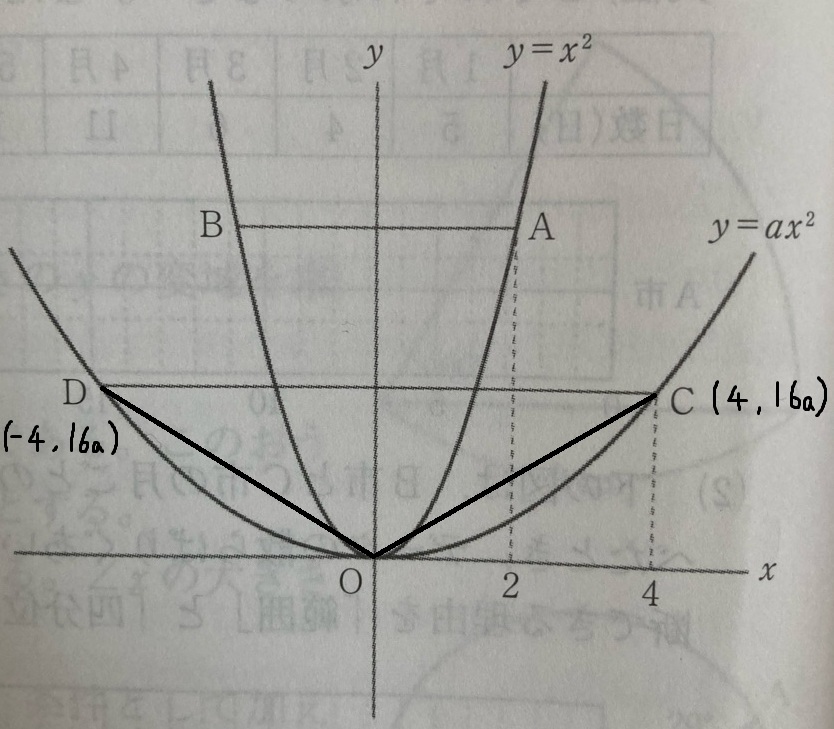
直線CD（底辺）＝8
高さ＝16a
三角形の面積＝底辺×高さ×1/2
△OCD＝8×16a×1/2
△OCD＝64a

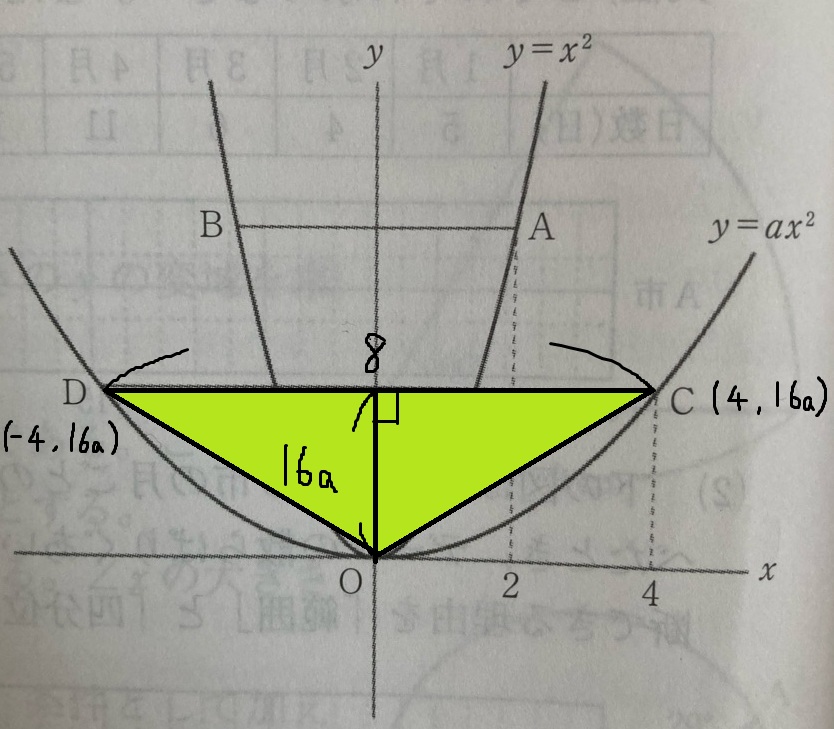
よって、△OCDの面積は64a

△OAB=△OCD
8=64a
64a=8
a=1/8

よって△OABと△OCDの面積が等しくなるときのaの値は
aの値は1/8

以上になります。
※意味や画像などはWikipediaなど、さまざまなサイト様を参考にしています。

本日もご覧くださり、ありがとうございました！

2022年　栃木県　公立高校入試問題　過去問　数学でした。次回からはこの続きを「かいせつ」していきます。

よろしくお願いいたします！

【学習塾トモニー】
塾のホームページが完成しました！もし興味がある方はぜひ、見ていただければと思います！完全自作になります！よろしくお願いいたします！