こんばんわ！

チャーハンを作ったら、足の親指を火傷してしまった眼鏡Pです。
＃なんで（笑）

では、2022年栃木県公立高校入試問題の過去問の数学を「かいせつ」していきます。

数学5⃣（関数）

（3）1/6
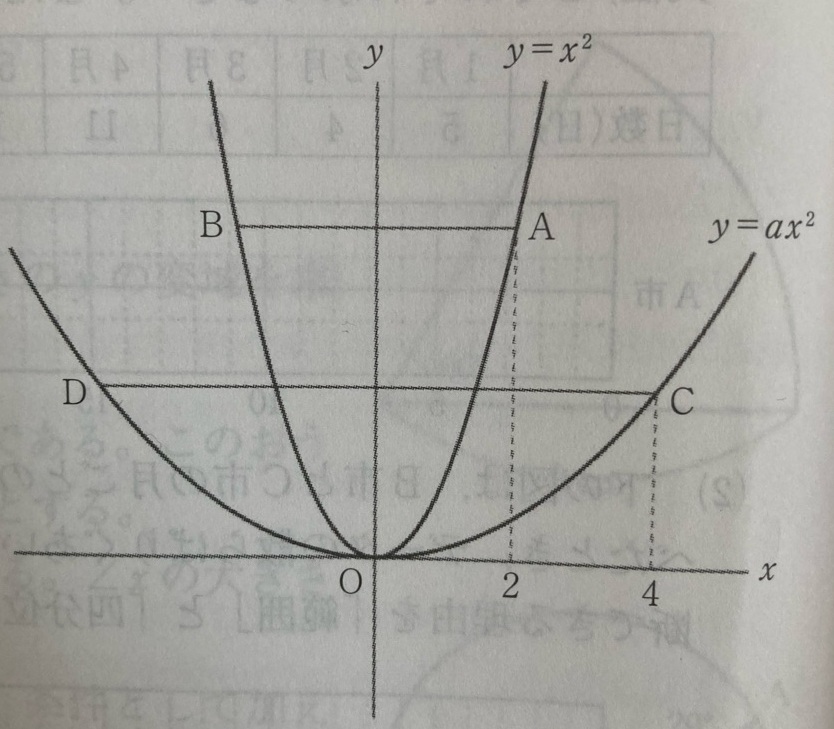
点Aと点Cを結ぶ直線AC
点Dと点Oを結ぶ直線DO
この2つの直線が平行になるときのaの値を求めたい。

直線が平行な時は、2つの直線の傾きが等しく。
※ちなみに、二次関数：y＝ax+bのとき傾きはaである。（ｂは切片）

そのために、まずは直線ACと直線DOを求めたい。
よって点A、点Ｃ、点Ｄを求める。

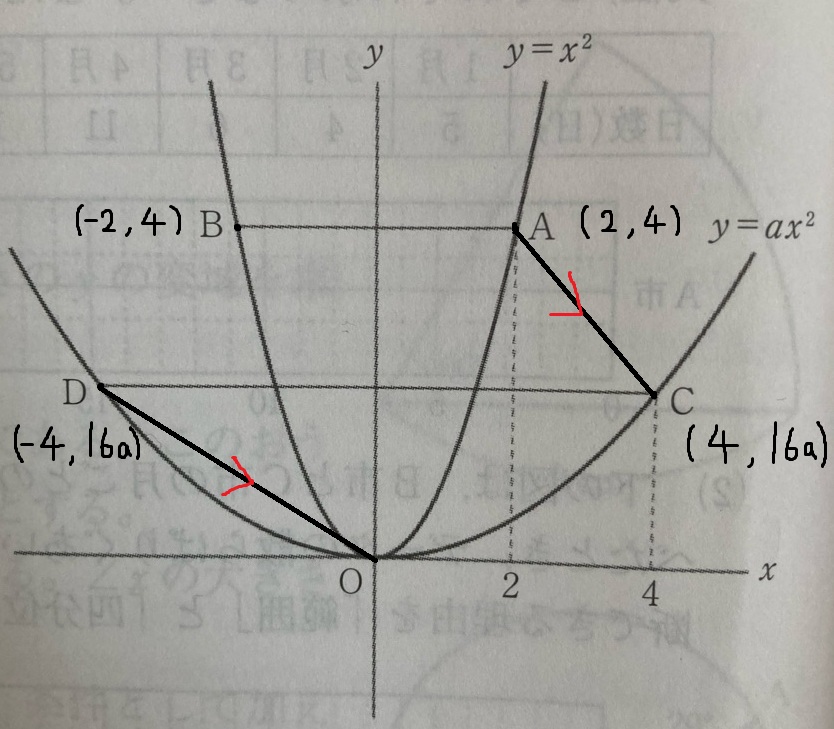
点Ａのｘ＝2より、ｙ＝ｘ²に代入するとｙ＝4
点Ａ（2、4）

点Ｃのｘ＝4より、ｙ＝aｘ²に代入するとｙ＝16a
点Ｃ（4、16a）

点Ｄのｘ＝ー4より、ｙ＝aｘ²に代入するとｙ＝16a
点Ｄ（ー4、16a）

傾き＝ｙの増加量/ｘの増加量

直線ＡＣの場合は
点Ａ（2、4）
点Ｃ（4、16a）

よって
ｘの増加量
＝2ー4
＝ー2

ｙの増加量
＝4－16a

直線ＡＣの傾き
＝4－16a/-2
＝-（4－16a）/2


直線ＡＣの傾き＝-（4－16a）/2


直線ＤＯの場合は
点Ｄ（ー4、16a）
点Ｏ（0、0）

よって
ｘの増加量
＝ー4ー0
＝ー4

ｙの増加量
＝16aー0
＝16a

直線DOの傾き
＝16a/-4
＝-16a/4
＝-4a


直線DOの傾き=-4a

直線ＡＣの傾き＝直線DOの傾き
-（4－16a）/2=-4a
4a=（4－16a）/2
8a=4－16a
8a+16a=4
24a=4
a=1/6

よってaの値は1/6となる。

以上になります。
※意味や画像などはWikipediaなど、さまざまなサイト様を参考にしています。

本日もご覧くださり、ありがとうございました！

2022年　栃木県　公立高校入試問題　過去問　数学でした。次回からはこの続きを「かいせつ」していきます。

よろしくお願いいたします！

【学習塾トモニー】
塾のホームページが完成しました！もし興味がある方はぜひ、見ていただければと思います！完全自作になります！よろしくお願いいたします！