おはようございます！

今日がテストラストの眼鏡Pです。
＃お疲れ様です！

では、2022年栃木県公立高校入試問題の過去問の数学を「かいせつ」していきます。

数学6⃣（特殊問題）
特殊問題のため、問題をそのまま画像にさせていただきました。

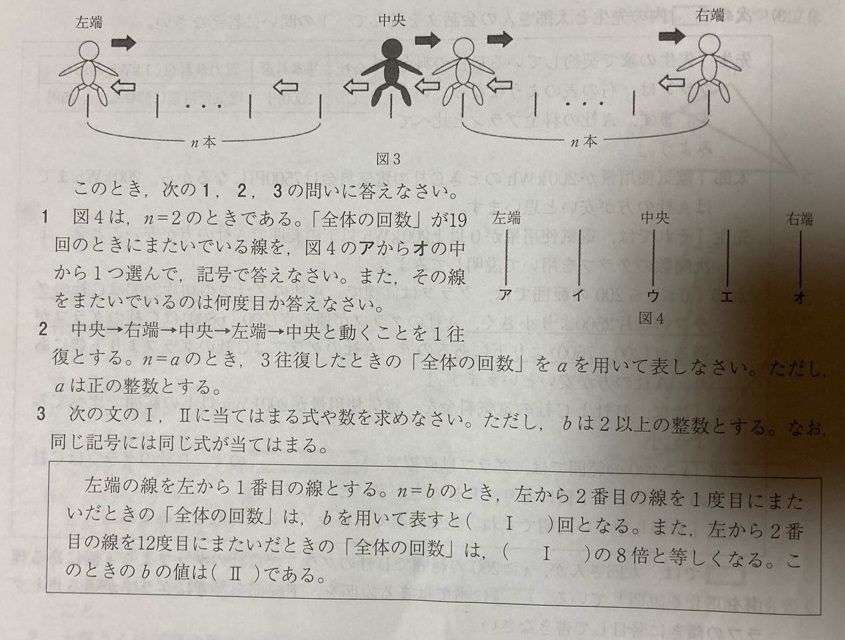
（3）b＝9
n＝bとすると
中央から右端まででb回
右端から中央まででb回
中央から左端まででb回
左端から中央まででb回
合計4b回線をまたぐ。

よって、1往復でまたぐ回数は4b回となり、これを5往復すれば4b×5＝20b回となる。

また、左から2番目の線は、中央から左端、または左端から中央へ向かう途中で1度ずつまたぐため、1往復あたり2回またぐことになる。

したがって、5往復すればこの線は2×5＝10回またぐことになり、11回目はその次、12回目はさらにその次の動きでまたぐことになる。このとき、12度目にその線をまたぐタイミングでの全体の線をまたぐ回数は、5往復分の20bに加え、

中央から右端までb回
右端から中央までb回
中央から左端までb回
さらに左端から中央へ向かう途中で1回またぐため
合計20b＋b＋b＋b＋1＝23b＋1回となる。

一方で、「左から2番目の線を1度目にまたいだときの回数」は、中央から右端（b回）、右端から中央（b回）、中央から左端（b−1回目でまたぐ）であるため、b＋b＋（b−1）＝3b−1回である。これを1単位として8回繰り返すと、（3b−1）×8回＝24b−8回。
この値と23b＋1が等しくなるので、
23b＋1＝24b−8
整理するとb＝9となる。

以上になります。
※意味や画像などはWikipediaなど、さまざまなサイト様を参考にしています。

本日もご覧くださり、ありがとうございました！

2022年　栃木県　公立高校入試問題　過去問　数学でした。
次が決まってません。
すみませんでした（泣）

よろしくお願いいたします！

【学習塾トモニー】
塾のホームページが完成しました！もし興味がある方はぜひ、見ていただければと思います！完全自作になります！よろしくお願いいたします！