おはようございます!
コミュ障の眼鏡Pです。
#上手くしゃべれないだよな(笑)
では、2024年北海道公立高校入試問題の過去問の数学を「かいせつ」していきます。

数学1⃣(小問集合)
問4
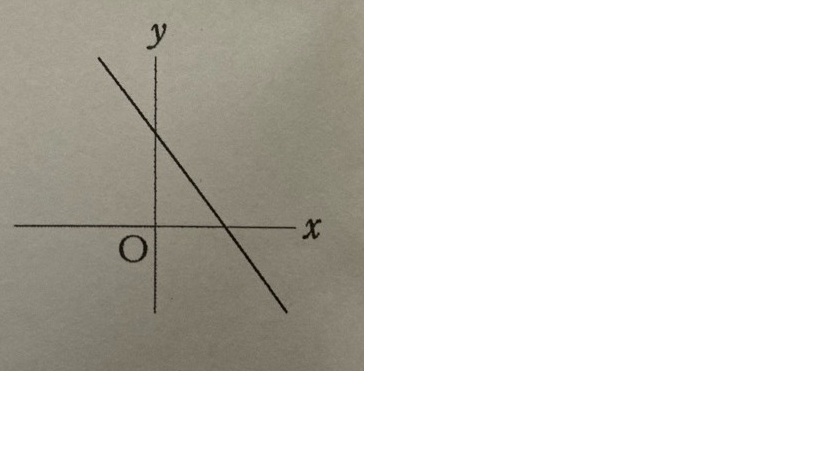
図のグラフは直線で、点O(原点)を通っていない。傾きa、切片bの符号について答える問題。
- 傾きaについて
右下がりの直線 ⇒ 傾きは負の数。
→ ア:正の数 × イ:0 × ウ:負の数 ○ - 切片bについて
y軸との交点(bの値)は、y軸の上側にある ⇒ 正の数
→ ア:正の数 ○ イ:0 × ウ:負の数 ×
答え:aの値は ウ、bの値は ア
問5
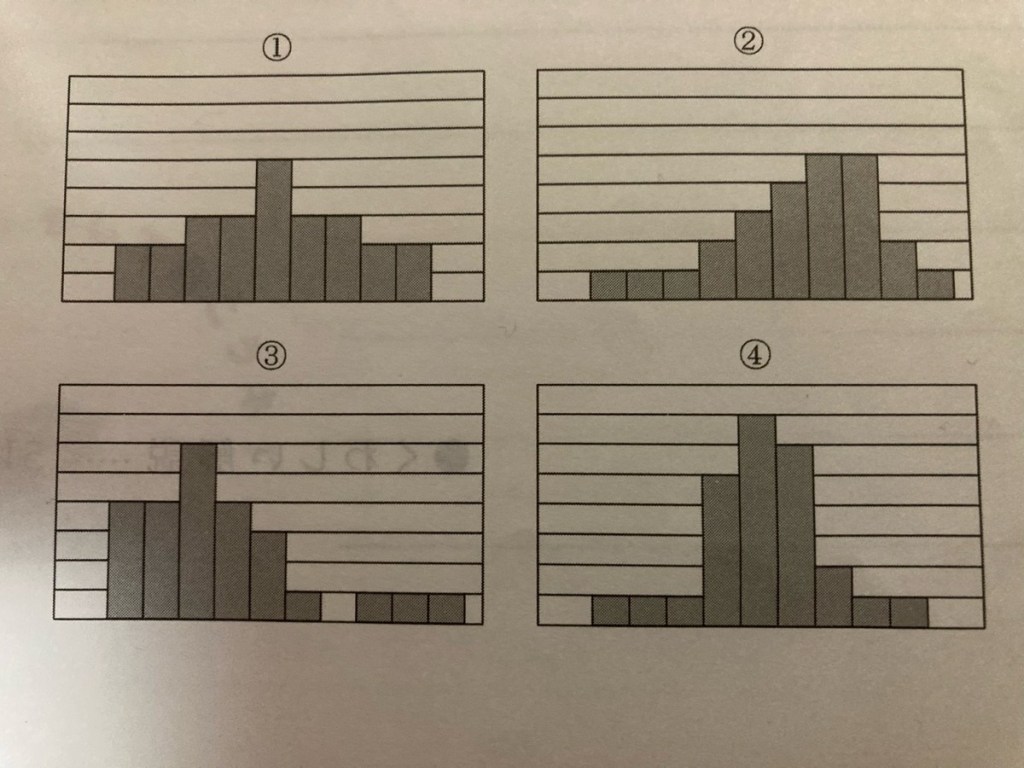
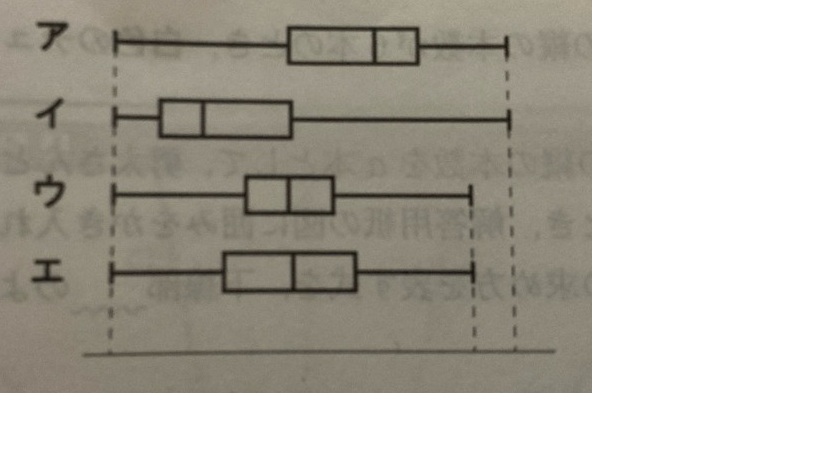
ヒストグラム①
- 特徴:左に山が集中(左にかたよっている)
- ⇒ 最頻値が左、右に長いひげ
- ⇒ 箱ひげ図「ア」(左寄り、右に長いひげ)
ヒストグラム②
- 特徴:左右対称な山型(平均・中央値・最頻値がほぼ同じ)
- ⇒ 標準的な形
- ⇒ 箱ひげ図「ウ」(中央値が中央寄り)
ヒストグラム③
- 特徴:右に山が集中(右にかたよっている)
- ⇒ 最頻値が右、左に長いひげ
- ⇒ 箱ひげ図「イ」(右寄り、左に長いひげ)
ヒストグラム④
⇒ 箱ひげ図「エ」(中央値がちょうど中央)
特徴:左右対称な形(②と同じくバランス型)
⇒ 中央に中央値、両端にそれほど極端な外れ値なし
答え:① ア、② ウ
問6
△ABPと△ACPの面積が等しい
⇒ 点Pは辺BCの中点になる必要がある。
作図手順:
その線と辺BCの交点が中点 ⇒ 点P。

コンパスでBとCを中心に同じ半径で円を描く。
2つの交点を結ぶと垂直二等分線。
以上になります。
※意味や画像などはWikipediaなど、さまざまなサイト様を参考にしています。
本日もご覧くださり、ありがとうございました!
2024年 北海道 公立高校入試問題 過去問 数学でした。次回からはこの続きを「かいせつ」していきます。
よろしくお願いいたします!
【学習塾トモニー】
塾のホームページが完成しました!もし興味がある方はぜひ、見ていただければと思います!完全自作になります!よろしくお願いいたします!