おはようございます！

お盆ロスになっている眼鏡Pです。
＃夏休みが終わった気がした（笑）

では、2024年北海道公立高校入試問題の過去問の数学を「かいせつ」していきます。

数学3⃣（関数）

問2

【問題】
点Pが関数 y = 2x² のグラフ上にあるとき、点Pの x 座標を t とする。点Qは点Pと x 軸について対称な点、点Rは点Pと x 座標が等しく、関数 y = (1/2)x² のグラフ上にある点とする。△PQRが直角二等辺三角形になるとき、t の値を求めなさい。

【解答】
t = 3/4

【かいせつ】

• 点Pの座標は (t, 2t²)
• 点Qは x 軸について対称なので (-t, -2t²)
• 点Rは関数 y = (1/2)x² 上の点なので (t, (1/2)t²)

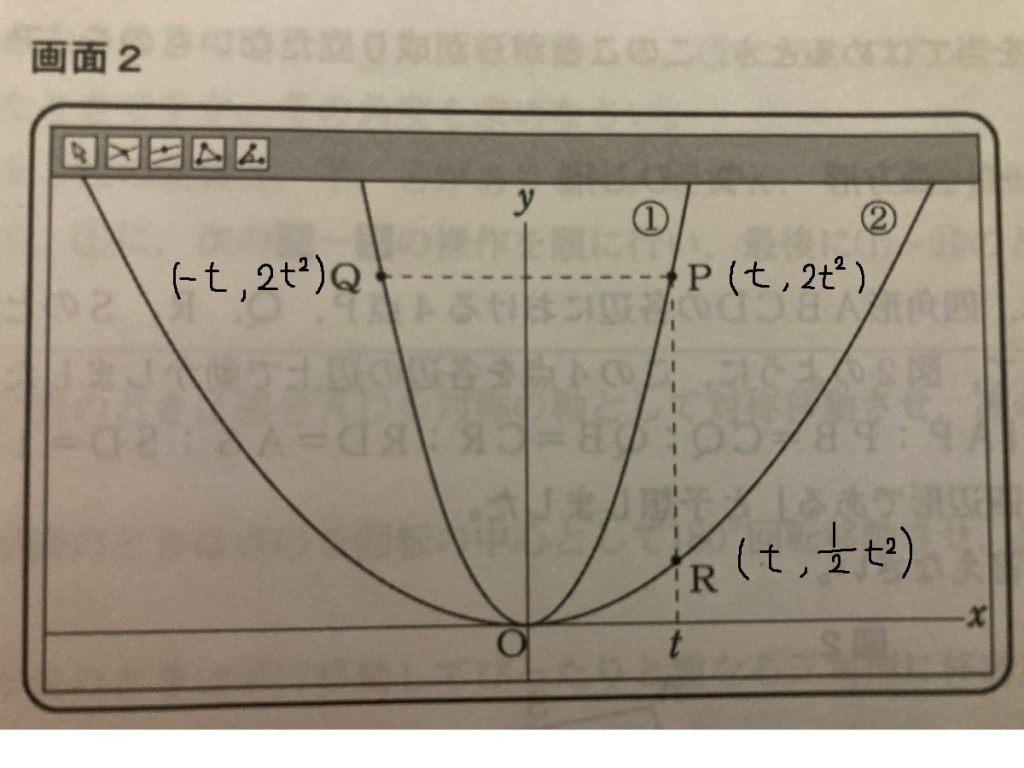
PQの長さ：
PQ
= （ｔ- (-ｔ)）
= 2ｔ

PRの長さ：
PR
= （2t² – (1/2)t²）
= (3/2)t²

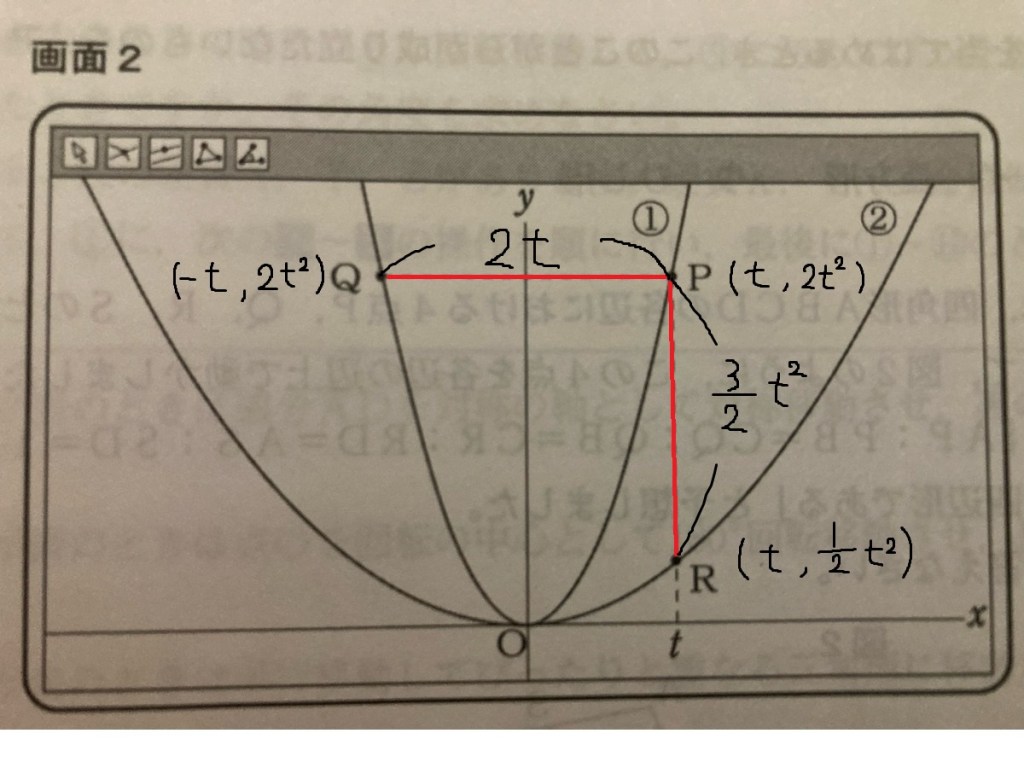
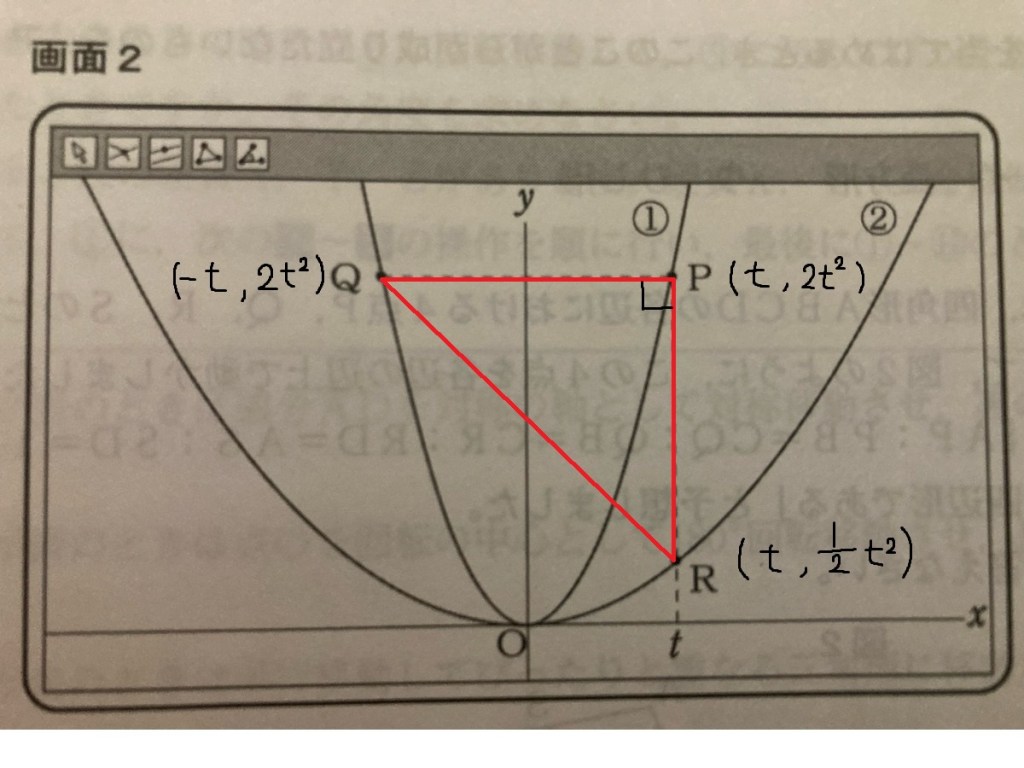
△PQRが直角二等辺三角形になる条件は PQ = PR
2ｔ = (3/2)t²
(3/2)t²＝2ｔ
(3/2)t²×2＝2ｔ×2
3ｔ²＝4ｔ
3ｔ²ー4ｔ＝0
ｔ（3ｔー4）＝0
ｔ＝0、4/3
（ｔ＞0）
よってｔ＝4/3

以上になります。
※意味や画像などはWikipediaなど、さまざまなサイト様を参考にしています。

本日もご覧くださり、ありがとうございました！

2024年　北海道　公立高校入試問題　過去問　数学でした。次回からはこの続きを「かいせつ」していきます。

よろしくお願いいたします！

【学習塾トモニー】
塾のホームページが完成しました！もし興味がある方はぜひ、見ていただければと思います！完全自作になります！よろしくお願いいたします！