こんばんわ！

フルーツバスケットのやり方を今日、知った眼鏡Pです。
＃今さら！？

では、2024年北海道公立高校入試問題の過去問の数学を「かいせつ」していきます。

数学4⃣（図形）

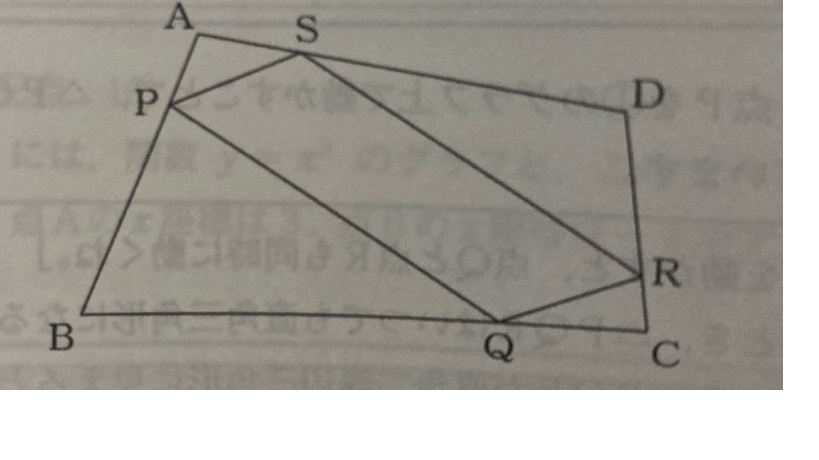
問1
解答　ア、ウ

四角形ABCDがひし形ならば、AC ⊥ BDより、
∠PQR = ∠QRS = ∠RSP = ∠SPQ = 90° となり、四角形PQRSはいつでも長方形である。よって、正方形とひし形にならない。

その特別な場合として、
四角形ABCDが正方形のとき、
・AC ⊥ BDかつ AC = BDより、
・∠PQR = ∠QRS = ∠RSP = ∠SPQ = 90°
・ PQ = QR = RS = SP となり、
四角形PQRSは正方形（ひし形）になる。

問2 (1) 証明（例1）
△APS と△ABD において、
AP : PB = AS : SD であるから、
PS //BD … (ア)

△CQR と △CBD において、
CQ : QB = CR : RD であるから、
QR / /BD … (イ)

(ア)，(イ) より、
PS : BD = AP : AB = 1 : 4 よって PS = 1/4 BD
QR : BD = CQ : CB = 1 : 4 よって QR = 1/4 BD

したがって PS = QR … (1)

よって、1組の対辺が平行で長さが等しいので、四角形PQRSは平行四辺形である。

（例2）
△APS と△ABD において、
AP : PB = AS : SD であるから、
PS //BD … (ア)

△BPQ と △BAC において、
BP : PA = BQ : QC であるから、
PQ ∥ AC … (1)

△DSR ∼ △DAC において、DS : SA = DR : RC であるから、
SR ∥ AC … (2)

(ウ)，(エ) より、PQ ∥ SR … (2)

(1)，(2) より、2組の対辺がそれぞれ平行なので、四角形PQRSは平行四辺形である。

以上になります。
※意味や画像などはWikipediaなど、さまざまなサイト様を参考にしています。

本日もご覧くださり、ありがとうございました！

2024年　北海道　公立高校入試問題　過去問　数学でした。次回からはこの続きを「かいせつ」していきます。

よろしくお願いいたします！

【学習塾トモニー】
塾のホームページが完成しました！もし興味がある方はぜひ、見ていただければと思います！完全自作になります！よろしくお願いいたします！