こんばんわ!
誕生日に色々と事件があった眼鏡Pです。
#前日に一番下の子が救急車
#当日には真ん中の子が腕を痛めて骨折したかと思うほど泣いて寝れず
#次の日には一番上の子が39°以上の高熱
では、2024年北海道公立高校入試問題の過去問の数学を「かいせつ」していきます。

数学1⃣(小問集合)
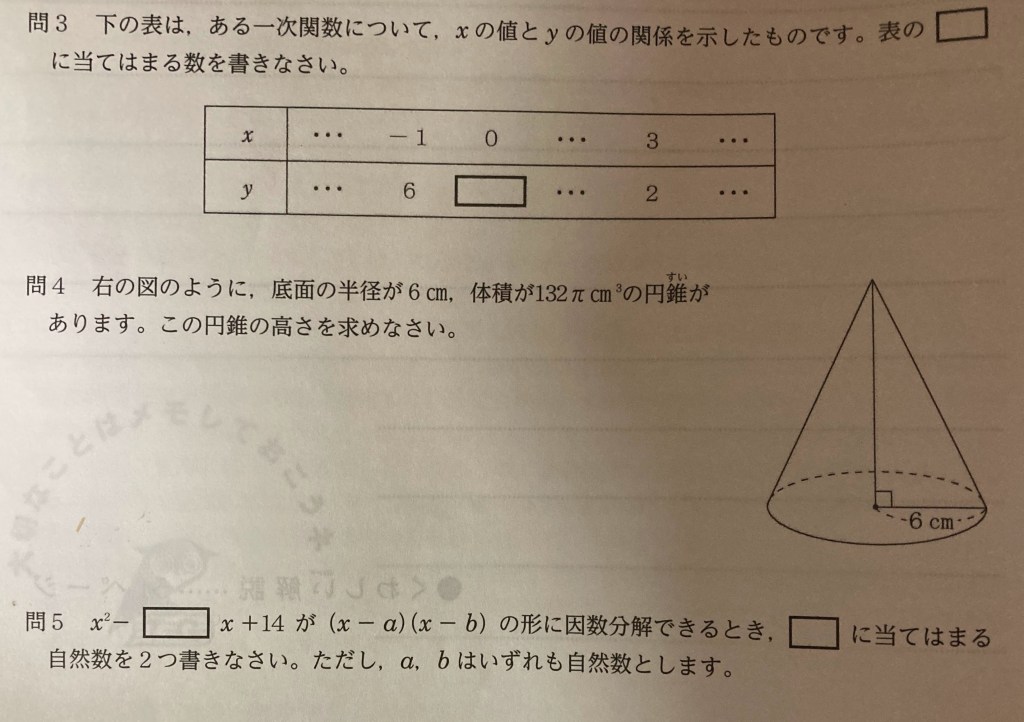
問3
【解答】 5
【解説】
x が −1 から 3 に変化するとき
3ー(-1)=4
xが4増えている。
y が 6から 2に変化するとき
2-6=-4
yは4減っている。
よって、
xが1増えるごとに
yは1減ることになる。
よって
6-1=5
問4
【解答】
高さ h=11 cm
【解説】
底面の半径が 6 cm
体積が 132π cm³ の円すい。
円すいの体積の公式より、
体積=1/3 × π × r² × h
132π = 1/3 × π × 6² × h
132π = 12πh
したがって、h=11 cm。
問5
【解答】
■に当てはまる自然数:9,15
【解説】
x² − ■x + 14 が、(x − a)(x − b) の形に因数分解できるとする。
展開すると、x² − (a+b)x + ab となる。
したがって、
ab=14
a+b=■
ab=14 を満たす自然数の組は、
(1,14)、(2,7)、(7,2)、(14,1)の4通りである。
それぞれに対して a+b を計算すると、
15、9、9、15 となる。
よって、■に当てはまる自然数は 9 と 15。
問6
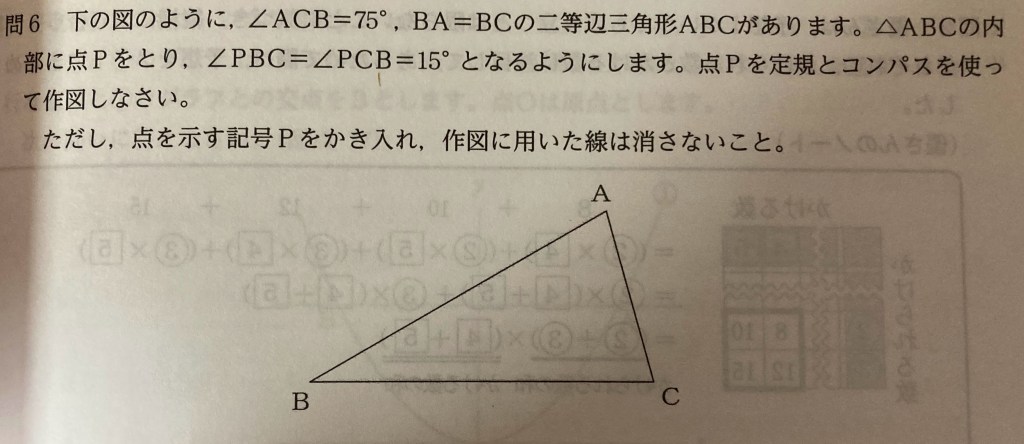
【解答のポイント】
∠PBC=∠PCB=15° より、△PBC は底辺 BC の二等辺三角形。
したがって、点 P は BC の垂直二等分線上にある。
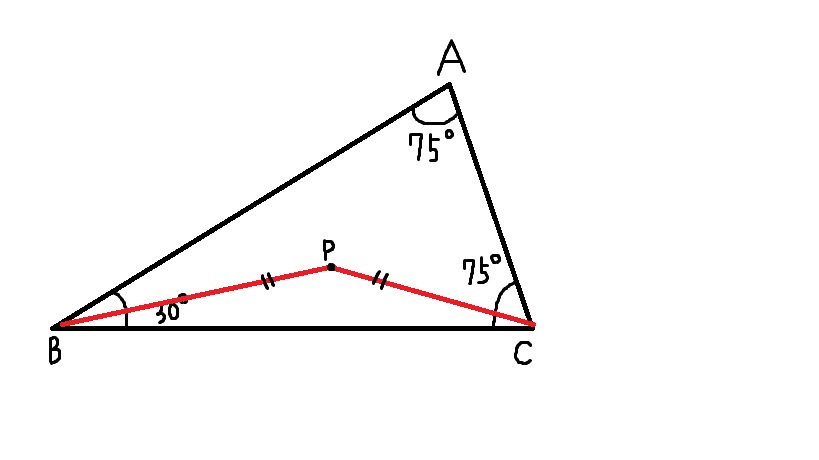
また、△ABC は BA=BC の二等辺三角形で、∠ACB=75°。
よって、∠ABC=180−75−75=30°。
∠PBC=15°=(1/2)∠ABC なので、点 P は ∠ABC の二等分線上にもある。
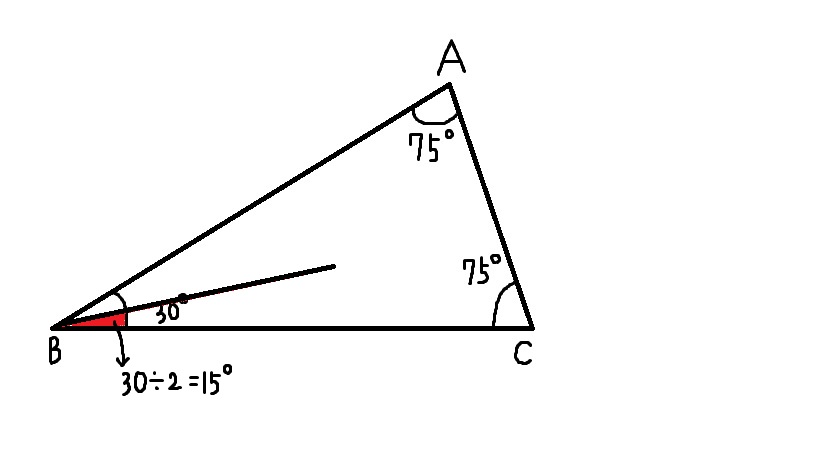
したがって、点 P は
「BC の垂直二等分線」と「∠ABC の二等分線」の交点。
【作図手順(定規・コンパス使用)】
① 辺 BC の垂直二等分線をかく。
・B、C を中心に、同じ半径で交わる円弧を2つ描く。
・交点2点を結ぶ直線を引く(これが BC の垂直二等分線)。
② ∠ABC の二等分線をかく。
・点 B を中心に弧を描き、辺 AB・BC との交点をそれぞれ E・F とする。
・E、F を中心に、同じ半径で交わる円弧を描く。
・その交点と点 B を結ぶ直線を引く(これが ∠ABC の二等分線)。
③ ①と②で引いた直線の交点を点 P とする。
・点名 P を書き入れ、作図に用いた補助線は消さない。
【解答】
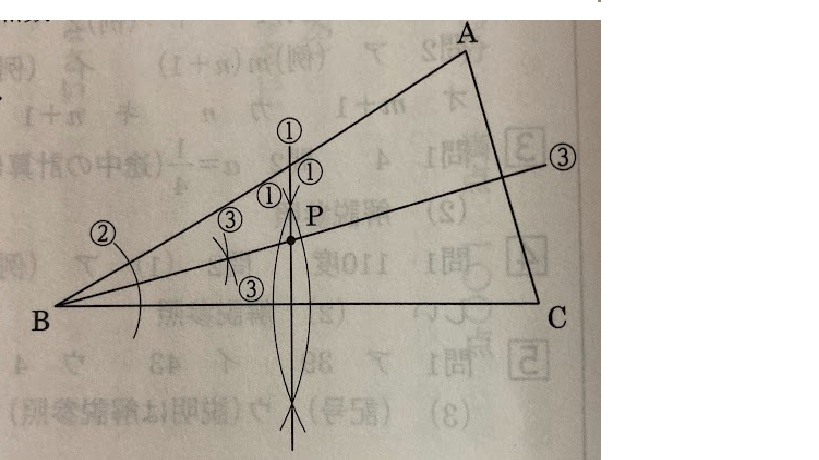
以上になります。
※意味や画像などはWikipediaなど、さまざまなサイト様を参考にしています。
本日もご覧くださり、ありがとうございました!
2024年 北海道 公立高校入試問題 過去問 数学でした。次回からはこの続きを「かいせつ」していきます。
よろしくお願いいたします!
【学習塾トモニー】
塾のホームページが完成しました!もし興味がある方はぜひ、見ていただければと思います!完全自作になります!よろしくお願いいたします!