こんばんわ！

世界中のお母さん、お父さんたちに聞きたいことがある眼鏡Pです。
＃子供たちが風邪をひいた時、どうしてるんですか！？

では、2024年北海道公立高校入試問題の過去問の数学を「かいせつ」していきます。

数学3⃣（関数）

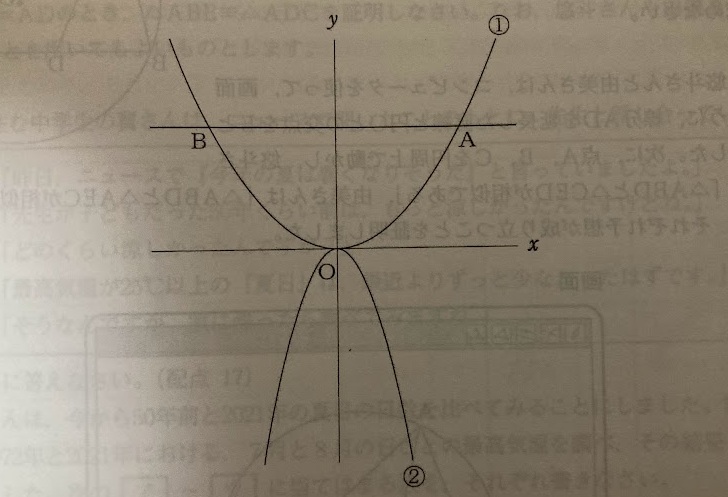
問1

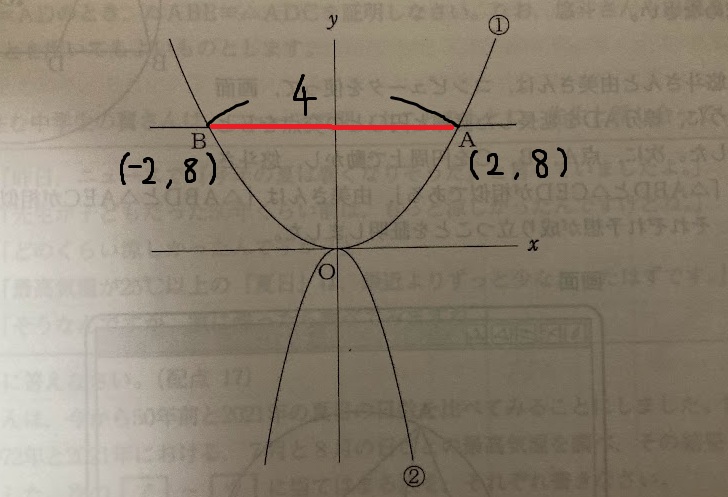
点 A は放物線
y=2ｘ²上にあるから、
y＝8 を代入して、
8 ＝ 2x²

x²＝4 より、x＝±2。

点 A の x 座標は正の数なので、x＝2。
したがって、A（2, 8）。

放物線は y 軸に関して線対称なので、
B（−2, 8）。

点 A と点 B の距離＝｜2 −（−2）｜＝4。

よって、点 A と点 B の距離は4

---

問2

関数 y＝a x² の変化の割合は、

ｘの値が1→3のとき、
y＝a x² にｘ＝1を代入すると
ｙ＝a×1²
ｙ＝a

y＝a x² にｘ＝3を代入すると
ｙ＝a×3²
ｙ＝9a

よって
ｘの値が1→3のとき、ｙの値はa→9aとなる。

ｘの値が1→3のとき、
ｘの増加量
＝3-1
＝2
ｘの増加量＝2

ｙの値はa→9a
ｘの増加量
＝9a-a
＝8a
ｘの増加量＝8a

変化の割合＝ｙの増加量÷ｘの増加量

8a÷2＝4a

一次関数
ｙ＝ｘ+2の変化の割合は1のため

4a＝1
a=1/4

---

問3

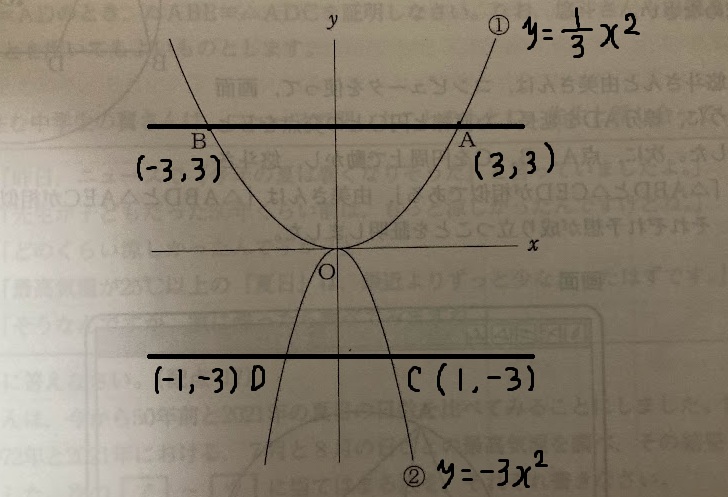
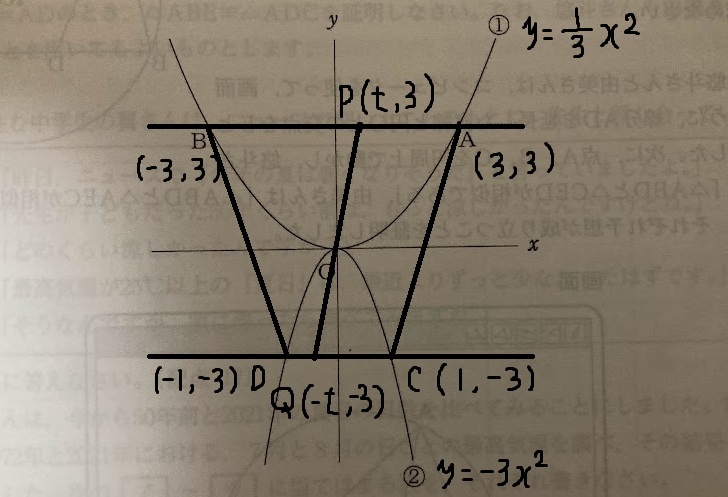
(1)
点 A は y＝3x 上にあるから、
y＝3x に x＝1 を代入すると、
y＝3 よって、A（1, 3）。

点 C は y＝−3x 上にあるから、
x＝1 を代入して、y＝−3。
したがって、C（1, −3）。

x 軸に平行な線分 AB 上にある点 P の y 座標は、
A の y 座標と等しいので、P（t, 3）。

直線PQは原点Oを通るため、
Q（-ｔ，-3）

---

(2)

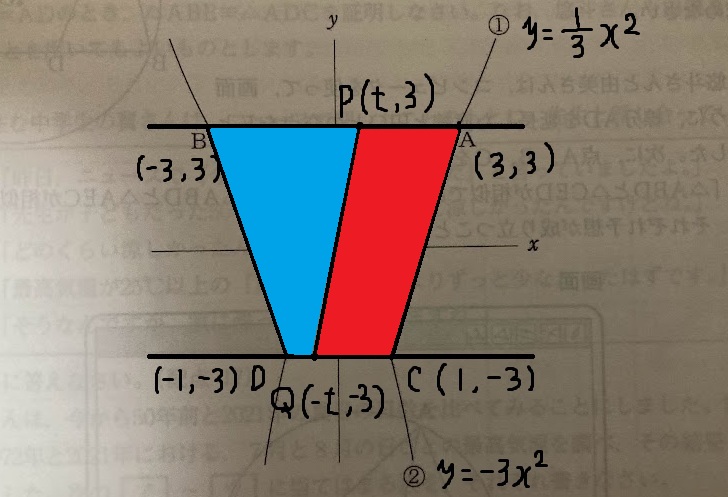
（台形 PQCA の面積）
＝（上底＋下底）×高さ÷2
＝（3＋1）×6×1/2＝12。 …①

（台形 ABDC の面積）
＝（6＋2）×6×1/2＝24。 …②

①②より、
（台形 PQCA の面積）＝（台形 ABDC の面積）×1/2

したがって、直線 PQ は台形 ABDC の面積を2等分する。

以上になります。
※意味や画像などはWikipediaなど、さまざまなサイト様を参考にしています。

本日もご覧くださり、ありがとうございました！

2024年　北海道　公立高校入試問題　過去問　数学でした。次回からはこの続きを「かいせつ」していきます。

よろしくお願いいたします！

【学習塾トモニー】
塾のホームページが完成しました！もし興味がある方はぜひ、見ていただければと思います！完全自作になります！よろしくお願いいたします！