おはようございます！

3連休最終日も頑張る眼鏡Pです。
＃よし！頑張るぞ！

では、2024年北海道公立高校入試問題の過去問の数学を「かいせつ」していきます。

数学4⃣（証明）

【問2】

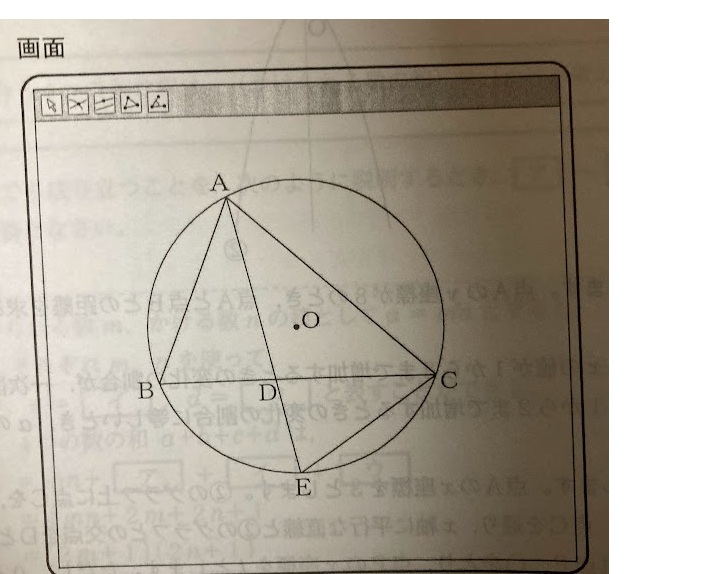
(1)
三角形の相似は、次のいずれかが成り立つときにいえる。
① 3組の辺の比がそれぞれ等しい
② 2組の辺の比とその間の角がそれぞれ等しい
③ 2組の角がそれぞれ等しい

悠斗さんと由美さんは、いずれも「2組の角がそれぞれ等しい」ことを示して証明した。

• 悠斗さんの証明
  弧ACに対する円周角は等しいので、
  ∠ABD＝∠CED
  対頂角は等しいので、
  ∠ADB＝∠CDE
  よって、2組の角がそれぞれ等しい
  
• 由美さんの証明
  弧ACに対する円周角は等しいので、
  ∠ABD＝∠AEC
  また、ADが∠BACの二等分線なので、
  ∠BAD＝∠EAC
  よって、2組の角がそれぞれ等しい

---

(2)（証明）

【例1】
△ABEと△ADCにおいて、
仮定より AB＝AD …①
ABに対する円周角は等しいので、∠BEA＝∠DCA …②
また、仮定より ∠BAE＝∠DAC …③

△ABE の内角の関係から、
∠ABE＝180°−(∠BEA＋∠BAE)
△ADC の内角の関係から、
∠ADC＝180°−(∠DCA＋∠DAC)

②③より ∠ABE＝∠ADC …④

①②③④より、1組の辺とその両端の角がそれぞれ等しいので、
△ABE≡△ADC

---

【例2】
（①までは例1と同様）
また、仮定より ∠BAE＝∠DAC …②
△AEC から対応する辺の比は等しいので、
AB：AD＝AE：AC＝1：1 → AE＝AC …③

①②③より、2組の辺とその間の角がそれぞれ等しいので、
△ABE≡△ADC

---

【例3】
（①までは例1と同様）
△ABD∽△AEC より、
AB：AD＝AE：AC＝1：1 → AE＝AC …②
△ABD∽△CED より、
AB：AD＝CE：CD＝1：1 → CE＝CD …③

仮定より ∠BAE＝∠EAC なので、
BEとCEの長さが等しい。

したがって、∠BCE＝∠EBC で、
△BEC は BE＝CE の二等辺三角形。

①②③より、3組の辺がそれぞれ等しいので、
△ABE≡△ADC

以上になります。
※意味や画像などはWikipediaなど、さまざまなサイト様を参考にしています。

本日もご覧くださり、ありがとうございました！

2024年　北海道　公立高校入試問題　過去問　数学でした。次回からはこの続きを「かいせつ」していきます。

よろしくお願いいたします！

【学習塾トモニー】
塾のホームページが完成しました！もし興味がある方はぜひ、見ていただければと思います！完全自作になります！よろしくお願いいたします！