こんにちは！

下仁田ネギの作業をしていると、泣いてしまう眼鏡Pです。
＃目にしみるwwww

では、2025年島根県公立高校入試問題の過去問の数学を「かいせつ」していきます。

数学1⃣（小問集合）　
【数学解説】

〈問6〉

図1のように，半径6cmの円Oの円周上に3点A，B，Pがあり，∠APB＝105°である。

1　図1の∠xの大きさを求める。

∠xは，点Pを含む弧ABに対する中心角である。
∠APBは，点Pを含まない弧ABに対する円周角であるから，この弧の大きさは
105°×2＝210° である。

円全体は360°なので，点Pを含む弧ABに対する中心角は
360°−210°＝150°

したがって
∠x＝150°

【答】150°

2　点Pを含む弧ABの長さを求める。

1より，点Pを含む弧ABに対する中心角は150°である。
円の半径は6cmなので，この弧の長さLは

L＝2π×6×150／360
　＝12π×5／12
　＝5π（cm）

【答】5πcm

―――――――――――――――

〈問7〉

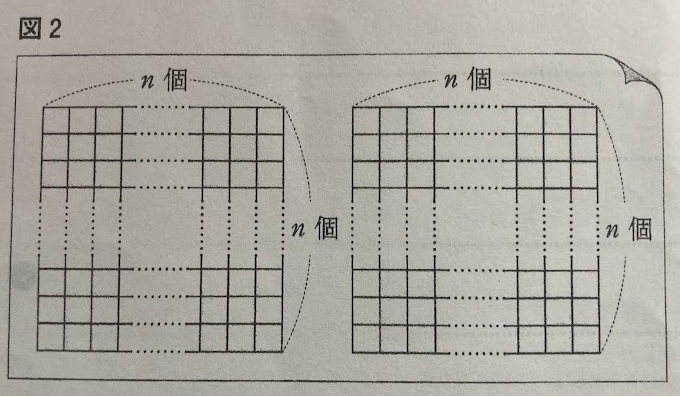
図2の用紙は，左右に同じ大きさのマス目がn個×n個ずつ印刷されている。
マス目1つに1字書くことができる。

1　n＝20のとき，用紙1枚に最大何字まで書くことができるか。

1つのマス目のかたまりは，たてnマス，よこnマスなので
1かたまりのマス目の数は n×n＝n² 個。

それが左右に2つあるので，用紙1枚のマス目の数は
2n² 個。

n＝20 を代入すると
2×20²＝2×400＝800

【答】800字

2　1枚に1000字書くことが可能な用紙のうち，最も小さいnの値を求める。

1より，用紙1枚に書ける字数は 2n² 字である。
1000字以上書ければよいので，

2n²≧1000
n²≧500

n²が500以上となる最小の自然数nを調べる。

22²＝484 ＜500
23²＝529 ≧500

したがって，条件をみたす最小のnは23である。

【答】23

―――――――――――――――

〈問8〉
アルミ缶とスチール缶の空き缶を合わせて2000個回収した。
この中から100個を無作為に取り出したところ，スチール缶が40個あった。

標本（100個）の中のアルミ缶の個数は
100−40＝60（個）

したがって，標本におけるアルミ缶の割合は
60／100＝0.6

母集団全体（2000個）でも，同じ割合0.6でアルミ缶があると考えるので，
回収したアルミ缶の個数xは

x／2000＝60／100

より

100x＝2000×60
100x＝120000
x＝1200

【答】ウ（1200個）

以上になります。
※意味や画像などはWikipediaなど、さまざまなサイト様を参考にしています。

本日もご覧くださり、ありがとうございました！

2025年島根県公立高校入試問題の過去問の国語でした。次回からはこの続きを「かいせつ」していきます。

よろしくお願いいたします！

【学習塾トモニー】
塾のホームページが完成しました！もし興味がある方はぜひ、見ていただければと思います！完全自作になります！よろしくお願いいたします！