こんばんは！

お腹が減った眼鏡Pです。
＃ラーメンでも食べたいよう（笑）

では、2025年島根県公立高校入試問題の過去問の数学を「かいせつ」していきます。

数学
5⃣

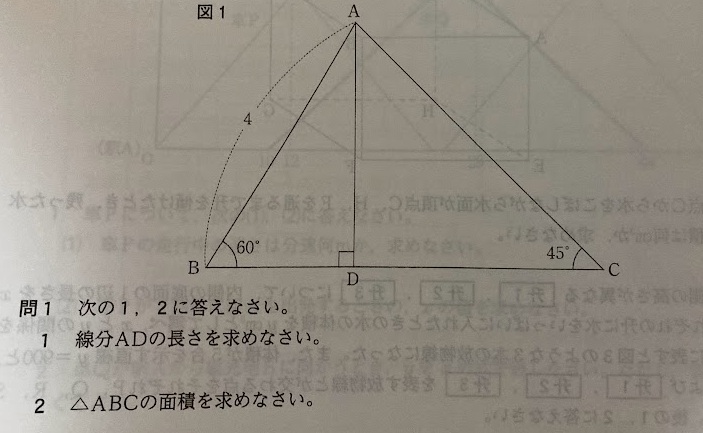
図1：AB＝4cm，∠B＝60°，∠C＝45°。
点Aから辺BCに垂線を下ろし，交点をDとする。

〈1〉線分ADの長さを求めなさい。
△ABDは∠D＝90°、∠B＝60°、＜C＝30°の直角三角形である。
AB＝4cmである。よって、比でいうと1：2：√3である。
BD＝2㎝のため、DA＝2√3㎝となる。

【答】AD＝2√3 cm

〈2〉△ABCの面積を求めなさい。

△ABCの面積＝底辺BC×高さAD÷2 を使う。
高さADは（1）より 2√3 cm。次に，底辺BCの長さを求める。

△ADCは直角二等辺三角形のため、AD=CD。
CD＝2√3㎝

③ BCと面積を求める

　BC＝BD＋DC
　　 ＝2＋2√3（cm）

△ABCの面積Sは

　S＝BC×AD÷2
　　＝(2＋2√3)×2√3÷2
　　＝(2＋2√3)×√3
　　＝2√3＋6
　　＝6＋2√3（cm²）

【答】6＋2√3 cm²

以上になります。
※意味や画像などはWikipediaなど、さまざまなサイト様を参考にしています。

本日もご覧くださり、ありがとうございました！

2025年島根県公立高校入試問題の過去問の国語でした。次回からはこの続きを「かいせつ」していきます。

よろしくお願いいたします！

【学習塾トモニー】
塾のホームページが完成しました！もし興味がある方はぜひ、見ていただければと思います！完全自作になります！よろしくお願いいたします！