こんばんは!
かかとが割れた眼鏡Pです。
#もうじいさんだよ(笑)
では、2025年島根県公立高校入試問題の過去問の数学を「かいせつ」していきます。

数学
5⃣
図2のように,点Bと点Dから辺ACに引いた垂線と辺ACとの交点をそれぞれE,Fとする。

〈1〉 △CFD∽△CEBであることを証明しなさい。
△CFD と △CEB において
BE⊥AC,DF⊥AC より,
∠CFD=∠CEB=90° …①
また,CFとCEはともにAC上にあり、CDとCBはともにBC上にあるので、
∠CDF=∠ECB …②
①,②より,2組の角がそれぞれ等しいから,
△CFD∽△CEBである。
〈2〉 3点A,B,Eを通る円の中心をOとする。
(1)点Oを作図して求めなさい。
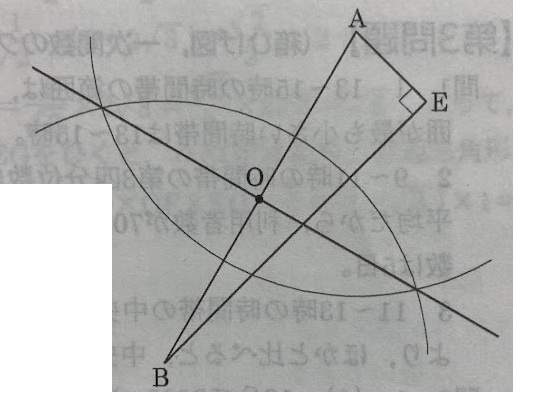
△AEB は,BE⊥AC,AとEがAC上にあるので,
∠AEB=90°である。
よって,3点A,B,Eを通る円では,ABが直径になり,
円の中心Oは線分ABの中点である。
したがって,
線分ABの垂直二等分線を引き,
その線とABとの交点をOとすればよい。
(2)線分OFの長さを求めなさい。

△ADC で,∠D=90°,∠C=45°なので,
△ADCは直角二等辺三角形である。
したがって,AD=DC=2√3 および
ACはその斜辺なので,
AC=2√3×√2=2√6
となる。
このとき,DF⊥AC でDが直角頂点なので,
DFは斜辺ACの高さであり,
直角二等辺三角形の性質から,FはACの中点となる。
よって,
AF=FC=AC/2=√6
一方,OはABの中点なので,
AO=OB=AB/2=2
△ABCにおいて,OはABの中点,FはACの中点だから,
OFは三角形ABCの中点連結線であり,
OF=BC/2
である。
問1の結果より,BC=2+2√3 なので,
OF=(2+2√3)/2
=1+√3
【答】OF=1+√3 cm
(3)△EOFの面積を求めなさい。
まず,EFの長さを求める。
(1)で示した相似より,△CFD∽△CEB なので,
対応する辺の比は
CF:CE=CD:CB
となる。
CD=2√3,CB=2+2√3,CF=√6 なので,
CE=CF×CB/CD
=√6×(2+2√3)/(2√3)
=√6×(1+√3)/√3
=√2(1+√3)
=√2+√6
したがって,
EF=CE−CF
=(√2+√6)−√6
=√2
次に,OFに垂直な線を点Eから引き,OFとの交点をGとする。
EG⊥OF なので,△EFGは直角三角形である。
また,FGはBCと平行,FEはACと平行なので,
∠EFGは∠ACB(=45°)に等しい。
∠EGF=90° より,残りの ∠EFG も45°となるから,
△EFGは45°−45°−90°の直角二等辺三角形
である。
よって,EFが斜辺なので,
EG=FG=EF/√2
=√2/√2
=1
最後に,△EOFの面積を求める。
OFを底辺,EGを高さとみると,
面積 = OF×EG÷2
= (1+√3)×1÷2
= (1+√3)/2
【答】△EOFの面積 = (1+√3)/2 cm²
以上になります。
※意味や画像などはWikipediaなど、さまざまなサイト様を参考にしています。
本日もご覧くださり、ありがとうございました!
2025年島根県公立高校入試問題の過去問の数学でした。次回からは2024年島根県公立高校入試問題の過去問の国語を「かいせつ」していきます。
よろしくお願いいたします!
【学習塾トモニー】
塾のホームページが完成しました!もし興味がある方はぜひ、見ていただければと思います!完全自作になります!よろしくお願いいたします!